Difference between revisions of "Heterozygosity"
| Line 5: | Line 5: | ||
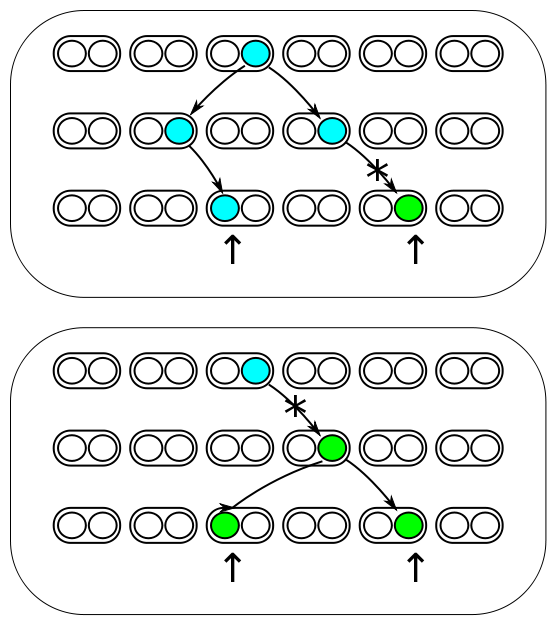
The image above represents three generations of a small population of six individuals per generation (N=6). Each individual is diploid and contains two copies of every gene in their genome (2N=12). Two gene copies are randomly sampled in the third generation and compared. There are two processes occurring each generation. Two lineages can come from the same copy in the generation before with a probability of 1/(2N) and therefor be identical to each other (and contribute to the overall rate of homozygosity in the population). Or a mutation could occur along one of the two lineages resulting in the gene copies being two different alleles from each other (and contribute to the overall rate of heterozygosity in the population). The probability of mutation is 2μ, where μ is the per generation per individual mutation rate; it is multiplied by two because a mutation could happen along either of the two lineages resulting in alleles being compared. | The image above represents three generations of a small population of six individuals per generation (N=6). Each individual is diploid and contains two copies of every gene in their genome (2N=12). Two gene copies are randomly sampled in the third generation and compared. There are two processes occurring each generation. Two lineages can come from the same copy in the generation before with a probability of 1/(2N) and therefor be identical to each other (and contribute to the overall rate of homozygosity in the population). Or a mutation could occur along one of the two lineages resulting in the gene copies being two different alleles from each other (and contribute to the overall rate of heterozygosity in the population). The probability of mutation is 2μ, where μ is the per generation per individual mutation rate; it is multiplied by two because a mutation could happen along either of the two lineages resulting in alleles being compared. | ||
| − | These are two competing processes and the important factor is which process happened last in the history of the two gene copies. The total probability of both events per generation is 2μ + 1/(2N). The probability the last event was a mutation out of the total (and thus heterozygous) is | + | These are two competing processes and the important factor is which process happened last in the history of the two gene copies. The total probability of both events per generation is 2μ + 1/(2N). The probability the last event was a mutation out of the total (and thus heterozygous) is |
| − | + | H = 2μ / (2μ + 1/(2N)). | |
| + | |||
| + | The rate of homozygosity is F = 1 - H, which is | ||
| + | |||
| + | F = 1/(2N) / (2μ + 1/(2N)). | ||
| + | |||
| + | We can rescale the terms in H by multiplying everything by 2N. | ||
| + | |||
| + | H = 2N 2μ / (2N 2μ + 2N 1/(2N)) = 4Nμ / (4Nμ + 1). | ||
| + | |||
| + | θ is often used to represent 4Nμ. | ||
| + | |||
| + | H = θ / (θ + 1). | ||
| + | |||
| + | This is the infinite alleles model, each mutation results in a new allele in the population. If θ is small relative to one then | ||
| + | |||
| + | H = θ / (θ + 1) ≅ θ / 1 = θ = 4Nμ. | ||
| + | |||
| + | H ≅ 4Nμ. | ||
(derivation from area and per generation effects) | (derivation from area and per generation effects) | ||
Revision as of 18:42, 15 October 2017
In population genetics heterozygosity is a measure of genetic diversity in a population. It represents an equilibrium between the input of genetic variation by mutation and the removal of variation by genetic drift.
The image above represents three generations of a small population of six individuals per generation (N=6). Each individual is diploid and contains two copies of every gene in their genome (2N=12). Two gene copies are randomly sampled in the third generation and compared. There are two processes occurring each generation. Two lineages can come from the same copy in the generation before with a probability of 1/(2N) and therefor be identical to each other (and contribute to the overall rate of homozygosity in the population). Or a mutation could occur along one of the two lineages resulting in the gene copies being two different alleles from each other (and contribute to the overall rate of heterozygosity in the population). The probability of mutation is 2μ, where μ is the per generation per individual mutation rate; it is multiplied by two because a mutation could happen along either of the two lineages resulting in alleles being compared.
These are two competing processes and the important factor is which process happened last in the history of the two gene copies. The total probability of both events per generation is 2μ + 1/(2N). The probability the last event was a mutation out of the total (and thus heterozygous) is
H = 2μ / (2μ + 1/(2N)).
The rate of homozygosity is F = 1 - H, which is
F = 1/(2N) / (2μ + 1/(2N)).
We can rescale the terms in H by multiplying everything by 2N.
H = 2N 2μ / (2N 2μ + 2N 1/(2N)) = 4Nμ / (4Nμ + 1).
θ is often used to represent 4Nμ.
H = θ / (θ + 1).
This is the infinite alleles model, each mutation results in a new allele in the population. If θ is small relative to one then
H = θ / (θ + 1) ≅ θ / 1 = θ = 4Nμ.
H ≅ 4Nμ.
(derivation from area and per generation effects)
(infinite allele derivation)
(infinite sites derivation using the coalescent)
(alternatives such as the stepwise mutation model for microsatellites)