Heterozygosity

In population genetics heterozygosity is a measure of genetic diversity in a population. It represents an equilibrium between the input of genetic variation by mutation and the removal of variation by genetic drift.

Infinite Alleles Model

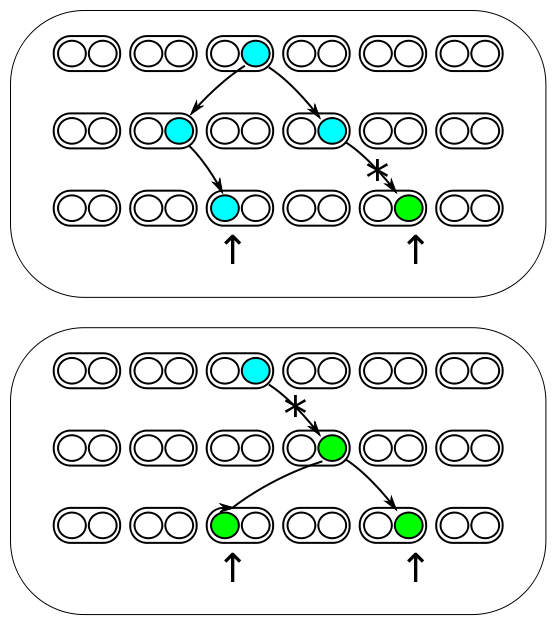
The image below represents three generations of a small population of six individuals per generation (N=6). Each individual is diploid and contains two copies of every gene in their genome (2N=12). Two gene copies are randomly sampled in the third generation and compared. There are two processes occurring each generation. Two lineages can come from the same copy in the generation before with a probability of 1/(2N) and therefore be identical to each other (and contribute to the overall rate of homozygosity in the population). Or a mutation could occur along one of the two lineages resulting in the gene copies being two different alleles from each other (and contribute to the overall rate of heterozygosity in the population). The probability of mutation is 2μ, where μ is the per generation per individual mutation rate; it is multiplied by two because a mutation could happen along either of the two lineages each generation resulting in the alleles being compared.

These are two competing processes and the important factor is which process happened last in the history of the two gene copies. The top panel shows a mutation (represented by an *) occurring after a mutation; thus the two copies are heterozygous when compared. The lower panel shows coalescence of the lineages after mutation; thus the copies are homozygous. The total probability of both events per generation is 2μ + 1/(2N). The probability the last event was a mutation as a fraction out of the total (and heterozygous in a direct pairwise comparison) is

[math]H = \frac{2\mu}{2\mu + 1/(2N)}[/math].

The rate of homozygosity is F = 1 - H, which is

[math]F = 1/(2N) / (2\mu + 1/(2N))[/math].

We can rescale the terms in H by multiplying by 2N/2N = 1.

[math]H = \frac{2N}{2N}\frac{2\mu}{2\mu + 1/(2N)}=\frac{2N 2\mu}{ 2N 2\mu + 2N 1/(2N)} = \frac{4N\mu}{4N\mu + 1}[/math].

θ is often used to represent 4Nμ.

[math]H = \frac{\theta}{\theta + 1}[/math].

This is the infinite alleles model, each mutation results in a new allele in the population. If θ is small relative to one then

[math]H = \frac{\theta}{\theta + 1} \approx \frac{\theta}{1} = \theta = 4N\mu[/math].

[math]H \approx 4Nμ[/math].

If θ is large relative to one then

[math]H = \frac{\theta}{\theta + 1} \approx \frac{\theta}{\theta} = 1 = 4N\mu[/math].

[math]H \approx 1[/math].

H increases approximately linearly with θ at small values but asymptotically approaches one (almost all pairwise comparisons are between different alleles) at higher values of θ.

Heterozygosity Area

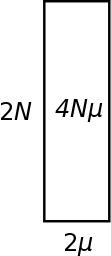
An alternative way to visualize heterozygosity (in terms of genetic diversity in a population) is as an area between 2N and 2μ. Genetic variation is lost by drift at a rate of 1/(2N). So the inverse of this, 2N, can be though of as the amount of genetic variation that is retained in a population and not lost to drift. As described above mutations that are relevant to heterozygosity (average pairwise comparisons) are input into a population at a rate of 2μ (where μ is the per generation mutation rate). The equilibrium level of genetic diversity as measured by heterozygosity is the product of the rate variation is added to a population and the amount of variation that can be maintained at any given time (think of this as almost like the size of a container, it can hold a certain amount before overflowing (or a funnel that drains slowly as new variants are added)); H = 2N 2μ = 4Nμ = θ.

Typically 2μ will be a very small number and 2N will be a very large number. Many orders of magnitude between these will cancel out as they are multiplied together. Also, you can see that a large population with a small mutation rate can have an equivalent level of genetic diversity as a small population with a high mutation rate.

Infinite Sites Model

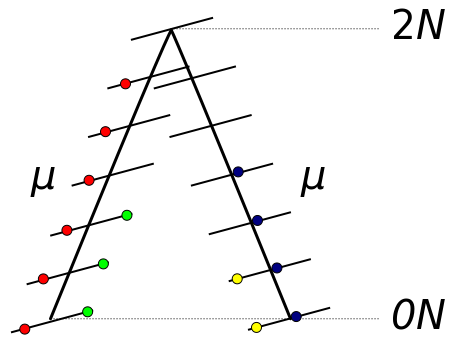
The probability of two ancestral lineages picking the same gene copy (coalescing) in the preceding generation is 1/(2N). The average amount of time until this takes is the inverse of the per generation probability or 2N generations. Therefore, on average two lineages will coalesce 2N generations in the past. If we track a DNA sequence that is inherited from a copy in the ancestor the two modern sequences will have an average of 4N generations between them (2N up to the ancestor and 2N down to the other copy). These generations are multiplied by the per generation mutation rate μ. A working assumption here is that each new mutation will change a different site or basepair along the DNA sequence (as if there were an infinite number of site to choose from). Therefore, the average nucleotide heterozygosity (the proportion of time two nucleotides are different in an alignment) within a population is H_n = 4Nμ.

In general per nucleotide mutation rates are very small and it is safe to assume that each new mutation within a population is likely to occur at a new basepair position. However, there are exceptions.

(give some examples of exceptions)

Stepwise Mutation Model

(example for microsatellites to be added)