Introduction to Genetics/Chapter 1. Introduction
Modern genetics can be divided into four main fields: quantitative genetics, classical genetics, population genetics, and molecular genetics. The following sections are a brief introduction to each of these fields, not that they are not integrated with each other and with other fields within and outside of biology. The concept of heritability is a good place to start in quantitative genetics. The connection between genotype and phenotype is used in classical genetics. Hardy-Weinberg genotype proportions introduce population genetics. And the flow of information from DNA to RNA to protein is mentioned in molecular genetics. Finally, the fields of statistics and genetics are closely connected, especially in a historical sense, and this is introduced with binomial probabilities.
Contents
Quantitative Genetics Introduction
A species is characterized by a range of traits such as height, length, pigmentation, weight, and growth rates. The genetic component of these traits can be quantified. These traits are called phenotypes and the amount of variation in the trait that is determined by genetic differences is called heritability. A classical example is human height. Stature is partially influenced by genetic variation and partially influenced by environmental factors such as health and nutrition. We tend to be more similar in height to our own parents than to unrelated people, but we cannot predict someone's height with perfect accuracy from their parents' height. Another overt example in humans is skin color. There is genetic variation that influences skin pigmentation. Again, children tend to be more similar to their parents in comparison to randomly selected people; however, there are also clear non-genetic environmental influences that influence skin color, such as exposure to ultraviolet light.
Let's switch gears and talk about something with no heritabilty to illustrate. We can roll two six-sided dice in a game of craps and add up the total from two (snake eyes) to 12 (boxcars). If we have fair dice the outcome of the first roll has no influence on the outcome of the second roll. The outcomes are only a result of physics: the speed, rotation, air drag, starting orientation, and friction with a surface. Dice have zero heritability (influence from previous rolls) and are only influenced by environmental effects. If we plotted the results from a first and second roll we do not expect a significant correlation in the sum of two dice.
A counter example is eye color in humans. Iris pigmentation due to the amount of melanin is almost completely explained by genetic variation inherited from our parents and has essentially no influence from the environment. If we scored the eye color of a large number of parents and offspring we expect a significant correlation because eye color is heritable and due to these genetic effects.
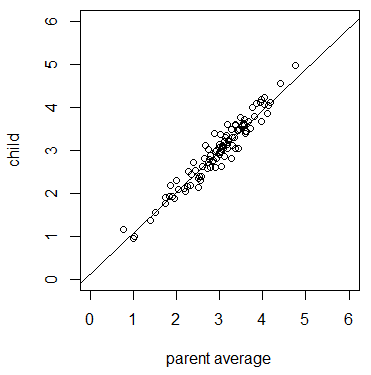
There are a wide range of traits in various species that have a range of heritability. Domesticated plant varieties and animal breeds are good examples. Phenotype variation selected by humans has increased the underlying genetic variation. Breeds have certain sets of unique traits because of a high heritability of these traits.
However, keep in mind that not all variation is heritable and due to genetic variation. American redstarts have variation in some of the feathers, from lighter yellow to darker orange-red, that is due at least in part to the availability of carotenoids in their diet and may indicate relative nutrition levels (Reudink et al., 2014).
Later I will write about how to quantify heritability, different types of heritability, how heritability can be used to make predictions in artificial selection experiments and some additional related topics.
Classical Genetics Introduction
Many species, such as humans and fruit flies, have two copies of most genes in their genome. There are tens of thousands of these genes across the genome. A gene can have different forms that alter the genes function. These forms of a gene are called alleles. Many tools come in different forms and this affects how they perform at different tasks. Some spoons are better for transferring liquid and some are designed to strain liquid. Some blades are used to carve wood and some are used to chop wood. These different forms can be thought of as alleles of a tool. Different tools are used to carry out different types of work; these tools can be thought of as genes which carry out different jobs within a cell. The collection of all the tools a family has can be metaphorically thought of as a genome. We often have spares or more than one copy of a single tool. In a similar way our genome has two copies of most genes. If one copy isn't working correctly there is usually a backup copy to carry out the function anyway.
Phenotypes are traits that are observed that derive from, at least in part, a genetic basis. It is important later on to remember that phenotypes are defined by humans based on what we can observe. Our height, the color of a tomato, the coat color of a dog are all phenotypes. The two alleles of a gene are together called a genotype. If the two alleles are the same this is a homozygote. If an individuals has two different alleles of a gene they are a heterozygote. There is a link between the genotype and the phenotype of an individual but this depends on the type of dominance of the phenotype and the relationship between the phenotype and the alleles.
A commonly encountered form of albinism in mammals is due to mutations at the albino gene (also called the c locus, locus is a synonym for gene in genetics, or the Tyr locus, named after the enzyme Tyrosinase produced by the gene). In classical genetics the common allele of the gene is called the wildtype allele and is symbolized by a capital letter C. An inactive mutant allele of the gene, that does not produce Tyrosinase, is symbolized by a lower case c. There are three possible genotypes that arise from these two alleles: CC, Cc, cc. Having one copy of the functional allele produces a sufficient amount of the Tyrosinase enzyme to have a wildtype coat color. So, both the CC homozygote and Cc heterozygote genotypes result in individuals with a wildtype brown coat color. Individuals with a cc genotype do not produce any Tyrosinase and have the recessive albino coat color.
The actor Peter Dinklage has achondroplasia which results in shorter limbs; a condition known as achondroplastic dwarfism. This is due to a mutation in the FGFR3 gene that causes an arginine amino acid to replace a glycine at amino acid 380 in the assembled enzyme. The mutation results on an overly active form of the protein and disrupts cartilage formation needed for the development of long limb bones. In this case the mutant allele (FGFR3[Gly380Arg]) results in a dominant phenotype; Peter Dinklage is heterozygous with a FGFR3[Gly380Arg]/FGFR3[+] genotype (here + indicates the non-mutant allele) and has only one copy of the disrupted allele. Homozygous individuals with FGFR3[Gly380Arg]/ FGFR3[Gly380Arg] genotypes do not survive early development. The same set of alleles can result in a range of phenotypes with a range of dominance. FGFR3[+] / FGFR3[+] homozygotes are expected to have regular stature. FGFR3[Gly380Arg]/FGFR3[+] have shortened limbs, a dominant phenotype. FGFR3[Gly380Arg]/ FGFR3[Gly380Arg] homozygotes do not survive, a recessive lethal phenotype.
The heterozygotes are the key to determining which phenotype is dominant. In the case of albinism Cc heterozygotes have brown fur so this is the dominant phenotype; a phenotype that is also shared with CC homozygotes. In the case of achondroplasia FGFR3[Gly380Arg]/FGFR3[+] heterozygotes have shortened limbs so this is a dominant phenotype and in this case the phenotype is not shared with FGFR3[+] / FGFR3[+] homozygotes.
The examples given here are cases of simple dominance where one phenotype is fully dominant or recessive to the other. There are a range of exceptions to this that will be discussed later. There are also different conventions used in naming and representing genes, alleles, and phenotypes. Two types have been used here with capital and lower case letters and designating the allele in brackets after the gene symbol (and using a + to indicate an non-mutant or wildtype allele). This will also be discussed more later on.
Population Genetics Introduction
(need to install the math extension to clean up the formatting in this section)
In some populations of Europe approximately four out of 1,000 people have haemochromatosis (high iron levels) because they are homozygous for a C282Y allele at the HFE gene (Hanson, 2001). The amino acid at position 282 in the protein encoded by HFE is changed from a cysteine to a tyrosine because a guanine base is changed to an adenine in the gene's DNA sequence. This disrupts the normal function of the HFE protein which plays a role in iron homeostasis. This iron overload causes organ damage if untreated. Fortunately, it is easy to treat by drawing blood but many cases are not identified before significant tissue damage occurs (OMIM #235200).
Haemochromatosis is a recessive phenotype. Based on the frequency of affected (homozygous) individuals what do we expect the frequency of carrier (heterozygous) individuals to be?
An allele is at a frequency, ppp, in the population. This frequency can be at any value from zero to one. If we randomly draw an allele from the population, say the allele an individual inherits from their mother, the probability that we picked a specific allele is equal to its frequency ppp. If the frequency of an allele is 1/2 then the chance of an individual inheriting one copy of the allele from their mother is 1/2. Some of those individuals will also inherit a copy from their father, again with a probability of 1/2. So half of the half of individuals have two copies. The frequency of these homozygotes is expected to be p×p=p2p \times p = p^2p×p=p2. In this example p = 1/2 so the frequency of homozygotes is 1/2 x 1/2 = 1/4.
If four out of 1,000 people are homozygotes we can use this to solve for the C282Y allele frequency p. p2=41000=0.004p^2 = \frac{4}{1000} = 0.004p2=10004=0.004 p=p2=0.004≈0.06p=\sqrt{p^2}=\sqrt{0.004}\approx0.06p=p2 =0.004 ≈0.06 So the frequency of the C282Y allele is expected to be about 6%. Now we need to use this to calculate the number of people that are expected to be heterozygotes. The frequency of all other alleles at this genes is 94% (1 - 0.06 = 0.94, this is 1 - p), for convenience we'll symbolize all other alleles with a "+". Each person has two chances to be a carrier because they have two alleles. An individual could be a heterozygote by inheriting the C282Y allele from their father and a + allele from their mother. The probability of this is 0.06 x 0.94 = 0.0564 (this is p(1-p)). Or, they could be a heterozygote the opposite way, by inheriting the + allele from their father and the C282Y allele from their mother. This probability is also 0.06 x 0.94 = 0.0564. Combining these together we get a probability (frequency) of heterozygotes of 0.0564 + 0.0564 = 0.1128 or about 11% of the population (this is 2p(1-p)).
Recessive conditions like haemochromatosis can have surprisingly high carrier frequencies. Four out of 1,000 people in Europe have haemochromatosis because they are homozygous for the C282Y allele. But, more than one in 10 people are expected to be carriers of the allele and can potentially pass it on to their children. If a child receives a C282Y allele from each parent then they are essentially certain to have haemochromatosis. We calculated this using what are known as Hardy-Weinberg genotype proportions. If an allele is at a frequency of p. Then homozygotes are expected to occur at a frequency of p2p^2p2 and heterozygotes at a frequency of 2p(1-p).
Does the model, based on math and logic, of expected genotype frequencies work? How close are these predictions to the frequencies in reality? (give example of tested frequencies)
Expected genotype frequencies is just the beginning of population genetics. As we have begun to see here, alleles can deviate from these expected proportions, vary in frequency among populations, and change in frequency over time. The forces of genetic drift, migration, mutation, selection, and recombination will be held for later.
Molecular Genetics Introduction
Genetics and Statistics Introduction
Glossary
Allele
Dominance
Environmental effects
Gene
Genetic effects
Genome
Genotype
Heritability
Heterozygote
Homozygote
Locus
Mutation
Phenotype
Wildtype
References
E. H. Hanson. HFE Gene and Hereditary Hemochromatosis: A HuGE Review. American Journal of Epidemiology 154, 193–206 Oxford University Press (OUP), 2001. Link
Matthew W. Reudink, Ann E. McKellar, Kristen L. D. Marini, Sarah L. McArthur, Peter P. Marra, Laurene M. Ratcliffe. Inter-annual variation in American redstart (Setophaga ruticilla) plumage colour is associated with rainfall and temperature during moult: an 11-year study. Oecologia 178, 161–173 Springer Nature, 2014. Link


