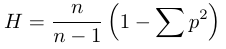Floyd A. Reed's Website: Heterozygosity, Small Sample Size Correction

Home > Science > Biology > Genetics > Population Genetics > Heterozygosity > Small Sample Size Correction

In small samples of genetic sequences there is a correction that is use where heterozygosity is adjusted upward by n/(n-1)

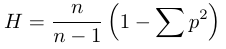where H is the heterozygosity estimate, p is the allele frequency, and n is the number of chromosomes, gene copies in a sample, or DNA sequences sequenced (not the number of individuals in a sample). See Schug et al. (1998) or Culvier et al. (2008) for examples of this in use.

Nei and Roychoudhury (1974) give this correction for estimates of homozygosity (one minus heterozygosity) in equation 2 of their paper. They state that the same is given in Mortin et al. (1971) and sometimes Nei (1987) is cited but I do not currently have access to either.

Why does this work? Image that 100 basepairs are sequenced from a single individual (n=2). Also imagine that there are four SNPs in the popualtion within the sequenced region at p=1/2 frequency.

The probability of two copies of an allele being heterozygous at this frequency is only 1/2. On average we only expect two of the sites to be heterozygous and our per-nucleotide heterozygosity estimate would be H = 2/100 = 0.02. However, because the sample size is so small we expect to have missed half of the sites (for the special case of p = 1/2). However, multiplying the estimated heterozygosity by the correction, n/(n-1) = 2/1 = 2, gives us an unbiased estimate of H = 0.04, or four out of 100 sites.

This correction quickly approaches one for larger sample sizes (e.g., 1.053 for n=20 or 10 diploid individuals) and is really only important when sample sizes are small.

(Note that this is in the same form as Bessel's correction for variance estimates from a sample.)

References

Culver, M., Hedrick, P. W., Murphy, K., O'Brien, S., & Hornocker, M. G. (2008). Estimation of the bottleneck size in Florida panthers. Animal Conservation, 11(2), 104–110. https://zslpublications.onlinelibrary.wiley.com/doi/abs/10.1111/j.1469-1795.2007.00154.x
Morton, N. E., Yee, S., Harris, D. E., & Lew, R. (1971). Bioassay of kinship. Theoretical Population Biology, 2(4), 507–524.
Nei, M. (1987). Molecular Evolutionary Genetics. New York: Columbia University Press.
Nei, M., & Roychoudhury, A. K. (1974). Sampling variances of heterozygosity and genetic distance. Genetics, 76(2), 379–390.
Schug, M. D., Hutter, C. M., Wetterstrand, K. A., Gaudette, M. S., Mackay, T. F., & Aquadro, C. F. (1998). The mutation rates of di-, tri-and tetranucleotide repeats in Drosophila melanogaster. Molecular Biology and Evolution, 15(12), 1751–1760.

Floyd A. Reed, January 4, 2020

About – Contact – Privacy