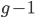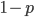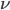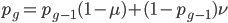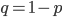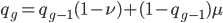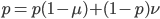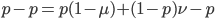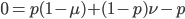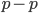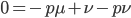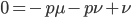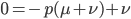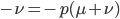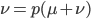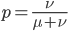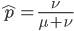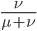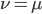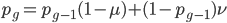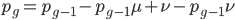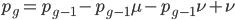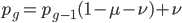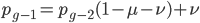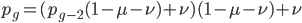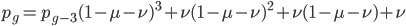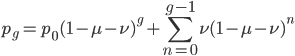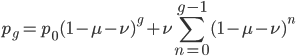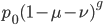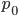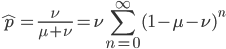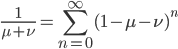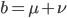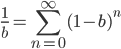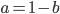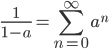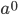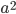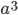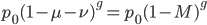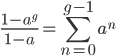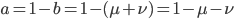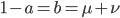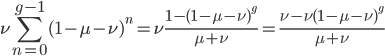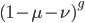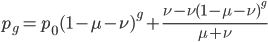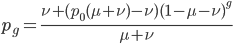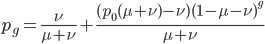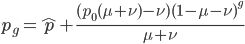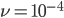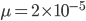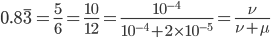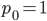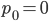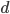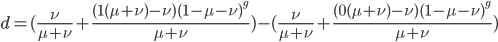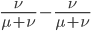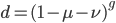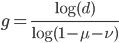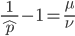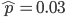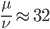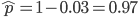Category Archives: mutation

Mutation-Selection Equilibrium

Leave a reply

How do you permanently increase or decrease the fitness of a population (in terms of population genetics). Is it better to intensify the strength of selection so that deleterious mutations are removed, or relax the strength of selection so that mutations are better tolerated. This is something that is relevant to the current human condition, where there is an increased amount of medical intervention and (in the very recent past) a relaxation of some adaptive demands in the environment (this will be misunderstood, human culture has placed additional demands upon humans in the longer timescale, but anyway...). Arguments can be made for either scenario and---it turns out that it really doesn't matter. Strangely enough the strength of selection cannot change the average fitness (at equilibrium) of a population.

For this post only think of mutations as deleterious (they lower an organism's fitness) if they have any effect at all. Most mutations either have no fitness effect (are selectively neutral) or lower fitness. Very few mutations in the genome would actually increase the fitness of an organism (adaptive).  Again think about making random changes to a car. Most changes, slightly reducing the length of the radio antenna, either make essentially no difference or, reroute the fuel line to the windshield wiper pump, are a very bad idea in terms of performance of the car. It would be very rare to make random changes that increase the performance of the car.

So, we know there are deleterious mutations that exist in a population that can result in what we identify in humans as a genetic disease. Many of these are recessive such as cystic fibrosis or Tay-Sachs disease; however, some are dominant such as Huntington's disease or Marfan's syndrome. And some do not fit this simple category such as X-linked hemophilia. Why do human and other species have so many deleterious alleles in the population?

The alleles are generated by mutation and removed by selection. We can have a mutation rate 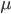and a strength of selection (relative to unmutated alleles) acting on those mutations . If we pretended the alleles acted independently, that pairing them together into diploid genotypes did not matter, then we can easily write down the equilibrium allele frequency, 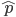, of the mutation.

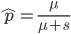
This is the rate that the allele is generated, 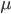, out of the total rate of input by mutation and removal by selection. For example, if the strength of selection against a mutant is 20% (a 20% fitness reduction relative to individuals with unmutated alleles) and the mutation rate is 0.1% then the equilibrium allele frequency is approximately one half of a percent, 0.5%. On the other hand if the fitness reduction is only 1% the allele can reach a higher frequency in the population at the same mutation rate (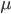=0.1%) the equilibrium becomes approximately 9%, which is a dramatically high frequency for a dominant deleterious allele. (This is mathematically equivalent to bi-directional mutation; however, here the "back mutation" to restore the original state is selection.)

Now lets keep track of genotypes and the case where the fitness effect of the allele is dominant (with some simplifying assumptions). If it is dominant and deleterious it is probably rare (not like the 9% case above), so homozygotes, 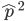are exceedingly rare and can be safely ignored because they contribute very little to the equilibrium dynamics. Mutations occur on the non-mutant allele copies 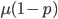(regardless if they are present in a homozygote or heterozygote). Selection removes a portion of heterozygotes, according to Hardy-Weinberg heterozygotes are expected to appear at a frequency of 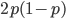and an fraction of these are removed so the genotype rate of removal is  .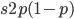

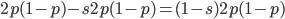(, the relative fitness to the unmutated homozygote is which adjusts the frequency of the heterozygotes 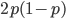 due to selection.)

Only half of the alleles in the heterozygotes are the mutant allele so the rate of removal of the mutant allele is 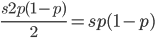. (Here we are focused on the case where the mutant allele is rare, which allows us to ignore 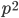in the first place. So, 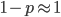. The frequency of heterozygotes is then approximately 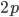. However, we want to keep track of the change in due to so we divide 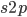by 2. Selection is also removing non-mutant alleles in heterozygotes but the non-mutant homozygotes are much more common so we just ignore the other half of the alleles that are removed due to selection; this comes from the assumptions of large population size and rare mutant allele frequency.)

At equilibrium the rate of input and removal of the mutation are equal.

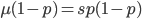
Rearrange and simplify.

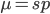
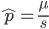
Using the two examples above with a mutation rate of 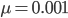the equilibrium allele frequency is predicted to be 0.5% for a fitness reduction of 20% and 10% for a fitness reduction of 1%, which is almost equivalent to the case where alleles are acted on independently (as haploids). (If then .)

What if the fitness effect is recessive? Then selection only removes the mutant homozygotes which are predicted to occur at a frequency of 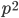. In this case selection can proceed more efficiently, in a sense, and mutant alleles are removed in pairs. All of the alleles in the homozygote are the mutant form so there is no adjustment necessary like dividing by two in the heterozygotes.

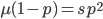
To keep this from getting messy let's use the trick now (which is actually less appropriate in this case because higher frequencies can be attained, but for now still assume that mutant alleles are very rare, , which is true for many mutations that result in human genetic diseases).

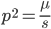
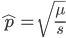
Using our two examples again, with a mutation rate of 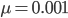the equilibrium allele frequency is predicted to be 7% for a fitness reduction of 20% and 32% for a fitness reduction of 1%. Now the equilibrium allele frequencies are much higher, when very rare (when ) the difference can be many orders of magnitude. Masking the fitness effects in heterozygotes (carriers) allows the allele to get to unexpectedly high equilibrium frequencies.

Now let's look at the average effect in the population. The average fitness 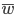in a population can be calculated as the fitness of each genotype multiplied by its corresponding frequency. Let's say the fitness of unmutated homozygotes is 100% or 1. In the case of a dominant fitness effect

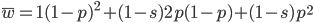
Expand and simplify

Let's say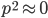

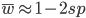
Substituting in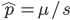

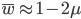
The average fitness is one minus twice the mutation rate.

On the other hand if selection is recessive

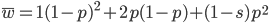
Expand and simplify

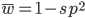
Substituting in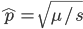

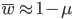
The average fitness is one minus the mutation rate.

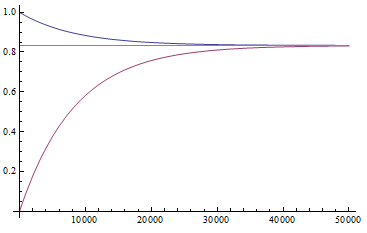
Interestingly, the average fitness in the population does not depend on the fitness of the genotypes within the population; it is only a function of the mutation rate! (However, it does depend on the type of dominance; recessive deleterious effects result in both a higher equilibrium allele frequency and a higher average fitness.) This seems like a paradox at first.  In our examples from above, if selection is dominant, then with a mutation rate of 0.1% the average fitness within the population is 99.8% regardless of how strong selection is against the mutation. If the mutation is recessive the average fitness is actually higher 99.9%, again regardless of the strength of selection against the mutation (this is related to selection being more efficient when it acts upon pairs of mutant alleles rather than one at a time in heterozygotes).

Why is average fitness only determined by the mutation rate? The trick to understand this is to realize that the strength of selection against a mutation and the frequency of the mutation in the population at equilibrium cancel out in terms of the average effect in the population. A mutation with a strong effect can only exist at a low frequency and only affect a few individuals, while a mutation with a weak effect attains a higher frequency and affects more individuals. The average effect of these two mutations, that have very different effects on fitness, in a population at equilibrium is the same.

However, going back to the original question of this post, changing the mutation rate can permanently change the average fitness of a population. How do you change the mutation rate? Well certain chemicals and radiation are well known examples. (Also, in a recent article Michael Lynch points out that if relaxed selection affects mutations in genes that affect the mutation rate itself, DNA repair, etc., then there could be a feedback effect where selection does influence equilibrium average fitness by altering the mutation rate.)

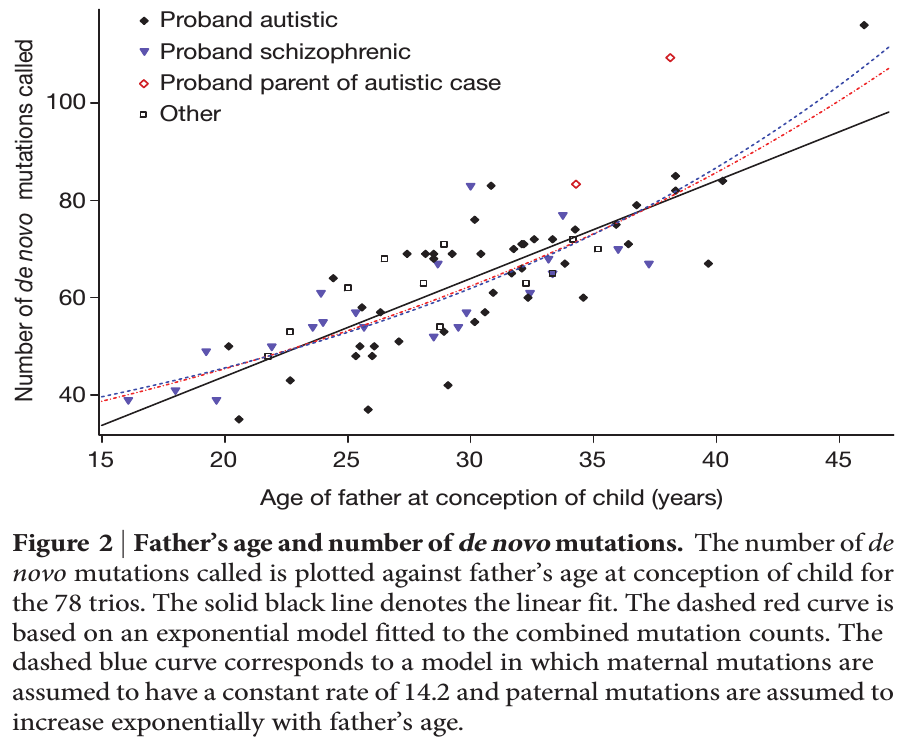
To put this in perspective, mutations are not rare unusual events that can safely be ignored; they affect all of us. We all have new mutations that can be passed on to our children. Whole genome sequencing estimates this as high as to be around 40-80 new mutations depending on the age of our father. (Click on the image below for the source information.)

newhumanmutations

Each year of father's age adds on average two new mutations. The age of the father is also a risk factor for diseases like autism and schizophrenia and new mutations might be playing a role.

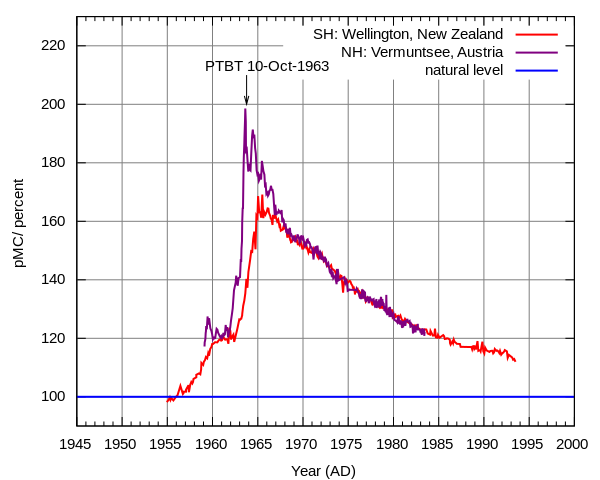
Above ground nuclear testing released large amounts of radioactive particles into Earth's atmosphere which spread planet-wide. At the height of the Cold War before the 1963 partial test ban the amount of radiation in the atmosphere was almost doubled (click on the image for a link to more information about how it was generated).

Radiocarbon_bomb_spike.svg

This had very real effects, for example it created a market for pre-war steel for specialized equipment like Geiger counters to test levels of radiation (steel made after WWII was contaminated with atmospheric radiation). A particularly valuable source are WWI battleship wrecks that are protected under water from contact with the atmosphere.

The increase in radiation alarmed some population geneticists like Hermann Muller who studied mutations and their effects on fitness. He helped raise awareness of the issue and his work among others contributed to the partial test ban treaty.

Furthermore, we come into contact with a wide range of industrial chemicals, many of which are seriously toxic and/or some of which can cause heritable mutations.

It is not known how this exposure might translate into increases in mutation rates (and to what degree this might contribute to the rates of genetic diseases). It would be interesting to estimate genome-wide mutation rates, in humans and other species if possible, over the last few centuries by comparing relatives sharing DNA sequences that are connected by different numbers of generations before and after certain points in history to see if there is a measurable effect.

Reversible Mutations

1 Reply

In the previous post about mutation predictions I only considered mutations in one direction (for example, from functional to non-functional gene sequences (while non-functional to non-functional mutations were ignored because the outcome is the same).)  However, some mutations can be thought of as reversible.  We could think of a nucleotide position mutating from an "A" to any other base-pair state ("C," "G," or "T") and then back again to an "A."  Or, we could think about changes in a codon that alternate between two different amino acids.  For example "CAT" and "CAC" both code for histidine while "CAA" and "CAG" both code for glutamine in the corresponding polypeptide (protein).  The only change is at the third position so a "T" or "C" is one amino acid and an "A" or "G" is the other.  As the sequence mutates and evolves between these four bases at this position we could think about this as reversible between two amino acid states.

aa-reversible-mutations

Another type of mutation is even closer to the sense of reversible.  Transposable elements are small stretches of DNA that can insert into a gene sequence, sometimes inactivating the gene, and then later excise out of the sequence, which might restore the original function.  In fact, transposable elements (or "TE's") are quite common in the genome of many organisms.  In the image below is an example from corn (in which TE's were first discovered).  Starting with an individual that has a TE inserted into a gene that produces the purple pigment (so no pigment is produced and the kernels are white) the TE can excise in certain cells (giving purple spots) and may even excise in the germ-line cells so that the next generation has completely restored pigment production.

nrg793-f1

We can write down the expected frequency in the next generation with reversible mutations as a recursion.  To be an allele at frequency in generation you are either already a type allele in the previous generation and did not mutate away with a mutation rate of (red) or you were the alternative allele at a frequency of and mutated at a rate of (blue).  (Incidentally, the "or" in the sentence implies that we add these two outcomes together rather than multiply because they are mutually exclusive; the allele either mutated or it did not; while the two "and"s in the sentence imply multiplying, the mutation rate and the allele frequency are independent events that have to co-occur to have the effect we are focusing on.)

.

We could also write this from the alternative alleles point of view .

.

Either way works the same in the end, but for the rest of this we are using the version.

At equilibrium so setting the allele frequencies between generations equal to each other gives:

.

Subtract from both sides to get the terms together.

Multiply everything out.

cancel out on the right

rearrange

factor

subtract from both sides

multiply both sides by negative one

solve for

This gives us the equilibrium allele frequency as determined by the forward and backward mutation rates.  Equilibrium values are often designated with a "hat" symbol like this:

From looking at this equation you can see the the equilibrium frequency of an allele is given by the mutation rate to the allele state as a fraction out of the total of the mutation rates, .  So for example, if is one half of the total rate of mutations (in other words if ) then . This seems to make intuitive sense, if different alleles are mutating into each other at the same rate, then over enough time the population will be made up of a 50/50 ratio of the alleles.

Going back to the original equation and multiplying everything out to rearrange the right hand side:

is this helpful?

substituting back in gives:

which is

which can be written in a summation series as

or (pulling out of the sum)

I'm not sure this is very helpful.  The sum on the right is hard to work with.  It would probably be easier to plot the change over time by simply iterating the original recursion equation.  However, one interesting thing about the equation above is the term goes to zero as becomes large because a large number of numbers less than one are being multiplied together.  This makes sense because as becomes large the equilibrium is approached and the initial condition matters less and less.  In fact, using this logic, and letting go to infinity, , we could write down:

dividing by gives:

which makes sense in the sense that the equilibrium allele frequency is only a function of the mutation rates (again the starting point should disappear because after an infinite number of steps toward a single equilibrium the result will be the same no matter where you started).

Is it known in general that this infinite series reduction pattern is true?  If we set then

becomes:

.

Then setting gives:

This is a classic result of an infinite sum of a geometric series.  (It is called geometric because raising to the is like adding dimensions in geometry.  is a point; is a line of length ; is a square with sides of length ; is a cube with edges of length ; etc.)

Also, looking at again.  If we have a total mutation rate then the first part of the equation, , is basically the same as the simpler model of irreversible mutation, .  So we can interpret the first part of this equation, , as the fraction of alleles that have not mutated yet.  Of course this will disappear as the equilibrium is approached.

Backing up to

and looking at the part on the right.  Now that we realize this is a geometric series we might be able to reduce the finite series.

A finite geometric series can be reduced by

            (link)

As above, substituting and realizing

.

Again, as goes to infinity goes to zero and becomes .

So, to be able to directly calculate the allele frequency at any point along the way as reversible mutations drive the system from a starting point toward equilibrium the equation is:

,

which can be simplified to:

.

This can be divided into an equilibrium component and a component quantifying the deviation from equilibrium due to the starting point and the time since starting :

or

Here is an example plot showing the predicted decline in allele frequency from 100% (blue) and the rise from 0% (red) compared to the equilibrium (yellow) where one mutation rate is a fifth of the other: and .  (Generations is on the x-axis and allele frequency is on the y-axis.)

reversible-mutation-example

So, by 50,000 generations, which again is not that long compared to geologic timescales, the allele frequency is predicted to essentially arrive at an equilibrium.  In this case we expect it to be

Exactly how long does it take to converge?  The allele frequency trajectories asymptotically approach equilibrium so they will never be exactly equal.  We could however ask when the difference is below a certain threshold.  If we start one and the other this is the largest difference, , we can begin with.  The difference between the two trajectories is (with zero and 1 substituted for in red):

We can immediately get rid of the difference in the equilibrium components , which is zero.  Also multiplying by one and zero simplifies the equation a little more.  Long story short, a lot cancels out and we end up with something familiar:

,

which makes a lot of sense.  We realized above that this was the fraction that had not yet mutated, which is the reason the curve deviates from equilibrium (i.e. starting points are different).

Solving for to get the number of generations gives us:

.

Plugging in the mutation rates from the example above we find that the difference in highest and lowest trajectories drops to less than 1% after 38,375 generations.

The probability that a transposable element inserts into a specific gene sequence is very small.  Once it is inserted (and sticking with simplistic assumptions here) the probability it will excise is likely much higher than the insertion in the first place.  Say we had data from huge fields of purple kernel color corn that had been maintained for many generations.  In, let's say, 3% of these we find a mutation due to a transposable element that prevents the pigment from being produced.  Assuming the population is at or very near to equilibrium what can we say about the insertion versus excision relative mutation rates?

can be rearranged to

.

Setting gives

So in this example, the excision rate is approximately 32 times higher than the insertion rate.  (If you define as the excision rate and as the insertion rate.  We can alternatively set and switch the symbols for the insertion and excision rates but the result is the same.)

Backing up to a more basic level, why is there an equilibrium at all?  We might also intuitively think that if one mutation rate is higher than the other that we would eventually end up with all of one type (allele) in the population.  (Actually this can happen when we start talking about drift in finite population but we are still ignoring that at the moment and pretending populations are so large that they are essentially infinite and even tiny fractions will be present.)  The trick to thinking about this is that as one allele becomes rarer it is a smaller target for mutations in the population.  As it becomes more common and in more copies there are more opportunities for mutations to occur to change the allele into a different form.  This frequency effect "buffers" the alleles towards intermediate frequencies, so an allele is never quite lost or fixed and we end up with an equilibrium.