Haldane 1937

Citation

Haldane, J. B. S. (1937). The effect of variation of fitness. The American Naturalist, 71(735), 337-349.

Links

• https://www.journals.uchicago.edu/doi/abs/10.1086/280722
• https://www.jstor.org/stable/2457289
• http://hawaiireedlab.com/pdf/haldane1937.pdf (internal lab link only)

Notes

Page 337

Paragraph One

Haldane points out the distinction between Darwinian evolution (novel adaptation) and stabilizing selection (or purifying selection or "maintenance" selection) that removes mutations which result in a phenotypic change.

Paragraph Two

The change in frequency of alleles resulting in novel adaptation can be very slow in human terms; however, extremely fast on a geologic timescale. Very small fitness differences in numbers of offspring could be virtually impossible to detect by direct observation yet have a very real evolutionary effect.

"In order that an observed viability difference of 0.1 per cent. should exceed twice its standard error, we should have to observe at least sixteen million individuals." If the average number of offspring per individual is two, for a population at constant size, this is expected to be Poisson distributed with a variance (σ²) of two.

Standard Error = [math]\frac{\sigma}{\sqrt{n}} = \frac{\sqrt{2}}{\sqrt{8,000,000}} = 0.0005 = 0.001/2[/math]

It is implied that two samples of size n=8,000,000, half with the genotype and half without, would be compared for a total of 16 million.

Paragraph Three

Again, adaptive evolution is expected to be very slow and not observable on a time-scale of human lifetimes (however, today we know of exceptions to this where observable evolution can happen quite rapidly). Except, Haldane says, possibly in cases of adapting to changes in the environment many of which are human caused, "agriculture, fishing and industry, the balance of nature has recently been upset in a manner probably without precedent in our planet's history; and hence on the Darwinian theory we should expect that evolution was proceeding with extreme and abnormal speed."

Page 338

Paragraph Four

The observation is made that in spite of selection against less fit (mutant) individuals in a species, and that this reduction in fitness is heritable, these individuals continue to appear at a roughly constant frequency over time, implying a deleterious-mutation-purifying-selection equilibrium.

Paragraph Five

Two different ways of thinking about fitness are defined, within a generation and over time.

First of all it is pointed out that the fitness of an individual is equal to half the number of offspring of that individual. A couple that have two children have a fitness of one. The number of individuals has been maintained as a constant number. [math]1\times2=2[/math]. If we focus on only a single parent then that individual has had two children and a fitness of one. Another way of thinking about it is from a single allele copy's perspective. A single copy in an individual has a 1/2 chance of being passed on to each offspring, so two offspring result in an even chance of the same number of copies of an allele in the next generation.

Within a generation the fitness of a genotype is the arithmetic average of half of the number of offspring of all individuals with that genotype. This seems to make intuitive sense and underscores that genotype fitness is an average effect over the population and not associated with any single individual.

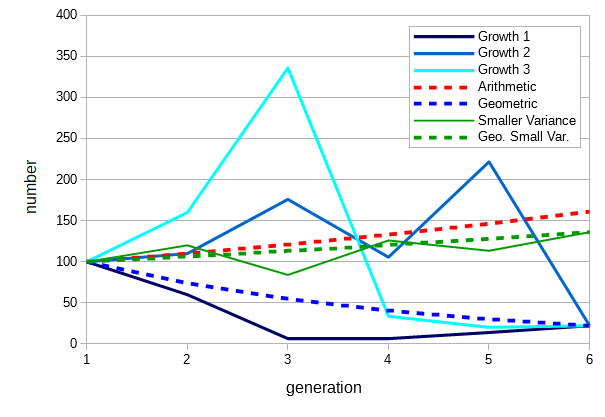
However, if the average fitness of an allele or genotype varies over time then its overall fitness is equal to its geometric mean over time, not the arithmetic mean. In order to illustrate here are replicates started with an initial 100 copies. The solid blue lines all have fitnesses over the generation of 0.1, 0.6, 1.1, 1.6, and, 2.1 but in different orders. These all have an arithmetic average of 1.1. However, if a constant fitness of 1.1 (increasing 10% each generation) is applied it results in a higher final number of copies (red dashed line). Rather, the blue lines all converge on a constant fitness of 0.74, which is the geometric mean of the fitnesses.

The geometric mean is always smaller than the arithmetic mean when there are differences in the constituent numbers being averaged. The degree to which it is smaller is related to the variance of the individual numbers. A series of fitnesses with the same arithmetic mean but with smaller variance results in a higher geometric mean over time (green lines). In this example a smaller variance in fitness over time results in a net increase compared to a larger variance with a net loss. This suggests that, all else being equal, selection will tend to favor alleles and genotypes that result in a smaller variance in fitness over time.

To be continued ...

Terms

• Facies - appearance. https://en.wiktionary.org/wiki/facies