Haldane 1937
Contents
Citation
Haldane, J. B. S. (1937). The effect of variation of fitness. The American Naturalist, 71(735), 337-349.
Links
- https://www.journals.uchicago.edu/doi/abs/10.1086/280722
- https://www.jstor.org/stable/2457289
- http://hawaiireedlab.com/pdf/h/haldane1937.pdf (internal lab link only)
Important Points
- Deleterious mutations are a constant presence and are expected to reach a mutation-selection equilibrium.
- The expected allele frequency of deleterious mutations with a dominant phenotype is [math]p\approx \mu/s[/math], where μ is the per generation mutation rate and s is the reduction in fitness (from one).
- The expected allele frequency of deleterious mutations with a recessive phenotype is [math]p\approx \sqrt{\mu/s}[/math].
- The average reduction in fitness due to dominant phenotypes is [math]2ps\approx 2 \mu[/math] and recessive phenotypes is [math]p^2 s\approx \mu[/math].
- In either case the average reduction in fitness in a population is independent of the strength of selection. This is because of a trade-off between the strength of selection and the allele frequency attained.
Notes
Page 337
Paragraph One
Haldane points out the distinction between Darwinian evolution (novel adaptation) and stabilizing selection (or purifying selection or "maintenance" selection) that removes mutations which result in a phenotypic change.
Paragraph Two
The change in frequency of alleles resulting in novel adaptation can be very slow in human terms; however, extremely fast on a geologic timescale. Very small fitness differences in numbers of offspring could be virtually impossible to detect by direct observation yet have a very real evolutionary effect.
"In order that an observed viability difference of 0.1 per cent. should exceed twice its standard error, we should have to observe at least sixteen million individuals." If the average number of offspring per individual is two, for a population at constant size, this is expected to be Poisson distributed with a variance (σ2) of two.
Standard Error = [math]\frac{\sigma}{\sqrt{n}} = \frac{\sqrt{2}}{\sqrt{8{,}000{,}000}} = 0.0005 = 0.001/2[/math]
It is implied that two samples of size n=8,000,000, half with the genotype and half without, would be compared for a total of 16 million.
We could think of this in terms of a t test to compare the two genotypes.
[math]t = \frac{0.001}{\sqrt{2}\sqrt{\frac{2}{8\times10^6}}}\approx 1.414[/math]
The corresponding one-tailed p-value of this t is 0.07868. So, an even larger number of individuals (approximately 1.083×107) would need to be compared to have a reasonable level of statistical confidence that one genotype has a higher fitness than the other.
Paragraph Three
Again, adaptive evolution is expected to be very slow and not observable on a time-scale of human lifetimes (however, today we know of exceptions to this where observable evolution can happen quite rapidly). Except, Haldane says, possibly in cases of adapting to changes in the environment many of which are human caused, "agriculture, fishing and industry, the balance of nature has recently been upset in a manner probably without precedent in our planet's history; and hence on the Darwinian theory we should expect that evolution was proceeding with extreme and abnormal speed."
Page 338
Paragraph Four
The observation is made that in spite of selection against less fit (mutant) individuals in a species, and that this reduction in fitness is heritable, these individuals continue to appear at a roughly constant frequency over time, implying a deleterious-mutation-purifying-selection equilibrium.
Paragraph Five
Two different ways of thinking about fitness are defined, within a generation and over time.
First of all it is pointed out that the fitness of an individual is equal to half the number of offspring of that individual. A couple that have two children have a fitness of one. The number of individuals has been maintained as a constant number. [math]1\times2=2[/math]. If we focus on only a single parent then that individual has had two children and a fitness of one. Another way of thinking about it is from a single allele copy's perspective. A single copy in an individual has a 1/2 chance of being passed on to each offspring, so two offspring result in an even chance of the same number of copies of an allele in the next generation.
Within a generation the fitness of a genotype is the arithmetic average of half of the number of offspring of all individuals with that genotype. This seems to make intuitive sense and underscores that genotype fitness is an average effect over the population and not associated with any single individual.
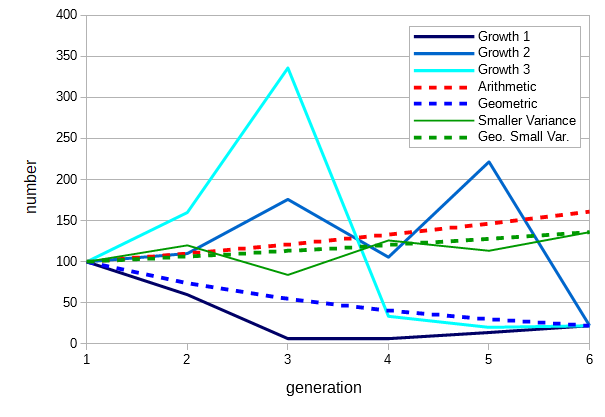
However, if the average fitness of an allele or genotype varies over time then its overall fitness is equal to its geometric mean over time, not the arithmetic mean. In order to illustrate here are replicates started with an initial 100 copies. The solid blue lines all have fitnesses over the generation of 0.1, 0.6, 1.1, 1.6, and, 2.1 but in different orders. These all have an arithmetic average of 1.1. However, if a constant fitness of 1.1 (increasing 10% each generation) is applied it results in a higher final number of copies (red dashed line). Rather, the blue lines all tend to decline over time and converge on a constant fitness of 0.74, which is the geometric mean of the fitnesses. (Transient losses are compounded more from lost potential future growth; this has a greater effect than transient gains.)
The geometric mean is always smaller than the arithmetic mean when there are differences in the constituent numbers being averaged. The degree to which it is smaller is related to the variance of the individual numbers. A series of fitnesses (1.2, 0.7, 1.5, 0.9, 1.2) with the same arithmetic mean, 1.1, but with smaller variance results in a higher geometric mean over time (green lines). In this example a smaller variance in fitness over time results in a net increase compared to a larger variance with a net loss. This suggests that, all else being equal, selection will tend to favor alleles and genotypes that result in a smaller variance in fitness over time. (Are stock investors and traders aware of this effect?)
Skipping Ahead
Page 342
Paragraph Seventeen
At equilibrium the rate of input of deleterious alleles by mutation is equal to the rate of removal by selection. μ is the per individual per generation mutation rate of interest and N is the number of diploid individuals in the population (the total number of gene copies is 2N). The rate of input is
[math]2N\mu-xN\mu = (2-x)N\mu[/math].
The is the total number of gene copies that mutate each generation, 2Nμ, minus the number of gene copies that have already mutated, xNμ.
The rate of removal is
[math]xN - fxN = (1-f)xN[/math],
where f is the fitness of individuals with a deleterious allele.
This is the number of individuals with a deleterious allele, xN, minus the ones remaining after selection has removed them, fxN. The strength of selection is s = 1-f.
At mutation-selection equilibrium these are equal,
[math](2-x)N\mu = (1-f)xN[/math],
[math]2N\mu-xN\mu = xN - fxN[/math],
[math]2N\mu = xN\mu + xN - fxN[/math],
[math]2N\mu = x(N\mu + N - fN)[/math],
[math]x = \frac{2N\mu}{N\mu + N - fN}[/math],
[math]x = \frac{2\mu}{\mu + 1 - f}[/math].
μ is much smaller than 1-f so the equation becomes
[math]x \approx \frac{2\mu}{1 - f}[/math].
x here is the number of heterozygous individuals. The deleterious allele frequency is assumed to be so rare that 1-x is approximately one and homozygotes are rare enough to be ignored. So x = 2p if p is the frequency of the deleterious alleles. Different mutations that disrupt gene function are grouped together into a deleterious allele class at a frequency of p.
Substituting s and p gives
[math]2p \approx \frac{2\mu}{s}[/math],
[math]p \approx \frac{\mu}{s}[/math].
If the loss of fitness is very small so that s is approaching the mutation rate μ then we can't ignore μ in the approximation above.
A slightly better approximation is
[math]p \approx \frac{\mu}{\mu+s}[/math]
which is the rate of input, μ, out of the total rates of input and removal, μ + s. If s is approximately equal to μ this approaches an allele frequency of 1/2, which means we can no longer assume [math]1-p \approx 1[/math] and
[math]2p(1-p) \approx 2\frac{\mu}{\mu+s}[/math],
[math]p(1-p) \approx \frac{\mu}{\mu+s}[/math],
is more accurate.
However, if s is much larger than μ the frequency of deleterious alleles is kept at a low frequency and
[math]p \approx \frac{\mu}{s}[/math]
works.
Interestingly, the loss of fitness in the entire population is the frequency of affected individuals times their corresponding fitness loss,
[math]x(1-f) = \frac{2\mu (1-f)}{1 - f+\mu} [/math].
If μ is small compared to 1-f,
[math]x(1-f) \approx \frac{2\mu (1-f)}{1 - f} =2\mu[/math].
The fitness loss is independent of the amount of selection against the deleterious allele; it is only a function of the mutation rate. At first this seems strange but realize that alleles with higher fitness attain a greater equilibrium frequency and have more of a net effect from their greater numbers in the population. Alleles with very low fitness are kept at low frequency in the population by selection. These two factors, frequency and fitness, largely cancel out and average fitness in the population becomes a function of mutation rates independent of the strength of selection.
If s is not much greater than μ average fitness in the population is affected by s.
[math]x(1-f) = \frac{2\mu s}{s+\mu} [/math].
Note
Haldane wrote
[math]x(1-f){,} = 2\mu - \frac{2\mu^2 (1-f)}{1 - f+\mu} \approx 2\mu[/math].
I agree that the 2μ2 term is very small compared to 2μ but at this time I do not see where it comes from.
Skipping Ahead
Page 344
Paragraph Twenty-one
Recessive deleterious phenotypes. Here x is the frequency of homozygotes and 2y is the frequency of heterozygotes.
The rate of input of new deleterious alleles by mutation is
[math]2N\mu - 2N\mu x - 2N\mu2y/2 = 2N\mu(1-x-y)[/math]
or the total number of newly mutated alleles minus the copies that have already mutated (which is half of the heterozygotes).
The rate of removal of deleterious alleles by selection is
[math]2Nx-2Nxf = 2Nx(1-f)[/math].
Note that each homozygote removed by selection removes two copies of a deleterious allele.
At equilibrium
[math]2N\mu(1-x-y) = 2Nx(1-f)[/math],
[math]\mu(1-x-y) = x(1-f)[/math],
[math]\mu-x\mu-y\mu = x-fx[/math],
[math]\mu-y\mu = x\mu + x-fx[/math],
[math]\mu-y\mu = x(\mu + 1-f)[/math],
[math]x=\frac{\mu(1-y)}{\mu+1-f}[/math].
If μ and y are small
[math]x\approx\frac{\mu}{1-f}[/math].
The average effect of loss of fitness over the population is
[math]x(1-f)\approx\frac{\mu(1-f)}{1-f}=\mu[/math].
Again this is independent of the fitness of the deleterious alleles and only a function of the mutation rate. The fitness cost and the frequency attained in the population cancel each other out.
Substituting p2 for x and s for 1-f gives
[math]p^2\approx\frac{\mu}{s}[/math]
and
[math]p\approx\sqrt{\frac{\mu}{s}}[/math].
A distraction into very weak selection
What if μ and y are not small? Substituting p and s
[math]x=\frac{\mu(1-y)}{\mu+1-f} = p^2 = \frac{\mu(1-p(1-p))}{\mu+s} = \frac{\mu-\mu p(1-p)}{\mu+s}[/math],
[math]p^2 = \frac{\mu}{\mu+s}-\frac{\mu p(1-p)}{\mu+s}[/math],
[math]p^2 +\frac{\mu p(1-p)}{\mu+s}= \frac{\mu}{\mu+s}[/math],
[math]p^2 +\frac{\mu p}{\mu+s} -\frac{\mu p^2}{\mu+s}= \frac{\mu}{\mu+s}[/math],
[math](\mu+s)p^2 +\mu p - \mu p^2= \mu[/math],
[math]\mu p^2+sp^2 +\mu p - \mu p^2= \mu[/math],
[math]p(\mu p+sp +\mu - \mu p)= \mu[/math],
[math]p= \frac{\mu}{\mu p+sp +\mu - \mu p}[/math],
[math]p= \frac{\mu}{p(\mu +s - \mu ) +\mu}[/math],
[math]p= \frac{\mu}{p s +\mu}[/math].
The equilibrium allele frequency is the mutation rate out of the total of the mutation rate and the allele removal rate of ps. Selection only acts upon the homozygotes so it is a function of the allele frequency p. The higher the frequency the closer ps is to s and selection is more efficient at removing alleles.
The average loss of fitness in the population is
[math]p^2(1-f) = s \left(\frac{\mu}{p s +\mu}\right)^2[/math].
[math]p^2(1-f) = \frac{s\mu^2}{(p s +\mu)^2} = \frac{s\mu^2}{p^2 s^2+ 2ps\mu +\mu^2}[/math].
[math]p^2(1-f) = \frac{s\mu^2}{(p s +\mu)^2} = \frac{s\mu^2}{p^2 s^2+ 2ps\mu +\mu^2}[/math].
μ2 is small.
[math]p^2(1-f) \approx \frac{s\mu^2}{p^2 s^2+ 2ps\mu} = \frac{\mu^2}{p^2 s+ 2p\mu} = \frac{\mu^2}{p(p s+ 2\mu)}[/math].
Substitute
[math]p= \frac{\mu}{p s +\mu}[/math]
in the right denominator.
[math]p^2(1-f) \approx \frac{\mu^2}{\frac{\mu}{ps + \mu}(p s+ 2\mu)} = \frac{\mu p s + \mu^2}{ps + 2 \mu}[/math].
μ2 is small.
[math]p^2(1-f) \approx \frac{\mu p s}{ps + 2 \mu}[/math].
This is messy but it does show that when selection is weaker relative to or approaching the mutation rate (allele frequency is high) the average effect in the population depends on s.
If 2μ is very small compared to ps we again get
[math]p^2(1-f) \approx \frac{\mu p s}{ps} = \mu[/math].
If ps is very small compared to 2μ we get (not very biologically reasonable, selection is very weak and the mutation rate is high)
[math]p^2(1-f) \approx \frac{\mu p s}{ 2 \mu} = \frac{p s}{ 2 }[/math],
in this case, since ps is very small, there is not much impact on average fitness. However, at this point other factors such as genetic drift in finite populations would likely dominate the dynamics. This is also getting close to the point where p is at intermediate frequency.
[math]p^2(1-f) = p^2s\approx \frac{p s}{ 2 }[/math],
[math]p\approx \frac{1}{ 2 }[/math].
Page 348
Haldane makes a statement about Eugenics: "This may be taken as a rough estimate of the price which the species pays for the variability which is probably a prerequisite for evolution. ... In other words, if we could achieve the aim of negative eugenics and abolish all genes (including autosomal recessives, most of which can not even be detected at present) which seriously lower fitness in our present environments, we might expect a gain in fitness of the order of 10 per cent., though this might lower our capacity for evolution in a changed environment."
To be continued ...
Terms
- Facies - appearance. https://en.wiktionary.org/wiki/facies