Michael Wallstrom presented his undergraduate research on a new marine species at the 41st annual Tester Symposium today.

I have neglected the genetics wiki on this site. One of the frustrations was not being able to write formulas correctly in the wiki markup code. However, I installed a SimpleMathJax extension and it allows TeX code to be added between <math> </math> tags. I added a genetic drift page to the site to test it out. http://hawaiireedlab.com/gwiki/index.php?title=Genetic_Drift

“His recipe for success is to have 4 problems on the go: a big problem, difficult and important, that will probably depress you before it makes you successful; a workable problem, tedious but with a clear strategy so you can always make some progress and feel a sense of accomplishment; a book problem, for the book you're writing or may eventually write; and a fun problem, since life is hardly worth living if you're not having some fun.” pp. 114-115 Genius At Play: The Curious Mind of John Horton Conway by Siobhan Roberts, Bloomsbury Publishing 2015

We submitted a preprint of our "network" manuscript to arXiv and it will post today (link and info below).  We also submitted it to a journal but went over the page limit so are currently editing it down to be shorter.

http://arxiv.org/abs/1509.02205

arXiv:1509.02205

Title: Stability of Underdominant Genetic Polymorphisms in Population Networks
Authors: \'Aki J. L\'aruson and Floyd A. Reed
Categories: q-bio.PE
License: http://arxiv.org/licenses/nonexclusive-distrib/1.0/

Heterozygote disadvantage is potentially a potent driver of population
genetic divergence. Also referred to as underdominance, this phenomena
describes a situation where a genetic heterozygote has a lower overall fitness
than either homozygote. Attention so far has mostly been given to
underdominance within a single population and the maintenance of genetic
differences between two populations exchanging migrants. Here we explore the
dynamics of an underdominant system in a network of multiple discrete, yet
interconnected, populations. Stability of genetic differences in response to
increases in migration in various topological networks is assessed. The network
topology can have a dominant and occasionally non-intuitive influence on the
genetic stability of the system. Applications of these results to theories of
speciation, population genetic engineering, and general dynamical systems are
described.

By the way, the is my first arXiv submission.  I wish I had done this years ago for other papers that were delayed for months, or in the two worst cases literally years, in review and resubmission cycles and then we ended up getting scooped in the end.  I am planning to use arXiv a lot more in the future.

It feels odd to submit something to be widely available before publication.  However, many journals now accept this (see also the discussion here) and there is excellent work that is freely available in arXiv.  There is also some discussion whether or not authors should cite preprints on arXiv with the general feeling that this is fine and in fact appropriate to do so and should be encouraged.

Jolene Sutton is starting a tenure track position as a new assistant professor in the Biology Department at UH Hilo this fall!

The Reed Lab now has an official twitter account! You can follow us @ReedLabHawaii.

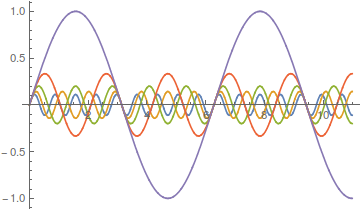
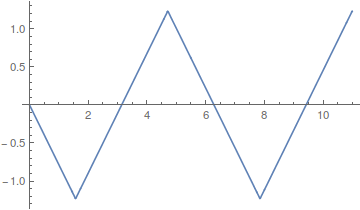
Lot's of different wave forms can be made by adding together harmonic series in certain ways.  A simple sine wave can have harmonics that vibrate twice as fast, three times as fast, etc.  Here is a plot of the odd numbered harmonics of a sine wave.

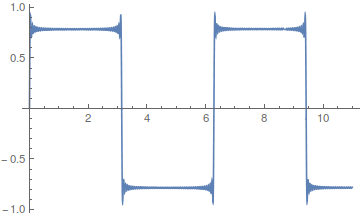
As the wavelength is reduced the amplitude of each wave is also purposely reduced.  It turns out that if you add these waves together you start approaching what is called a square wave.

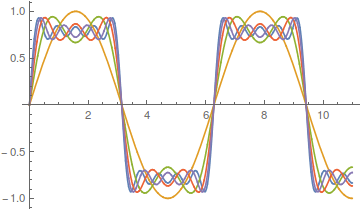
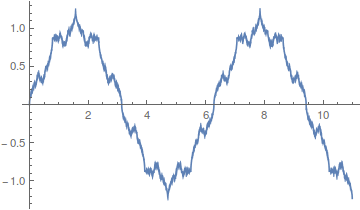
However, the approach can be slow.  There is a lot of wiggle in the waveform.  Below is a plot with 50 odd numbered harmonics added together; .

Closer, but you can still see the oscillation at the height of each peak.

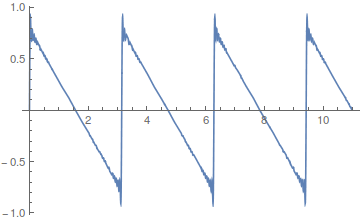
If you add together the even harmonics, , you get a sawtooth wave.

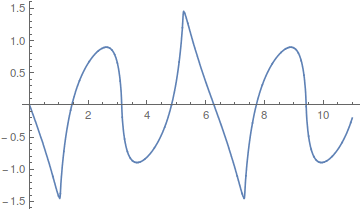
Odd harmonics with a different weighting scheme, , give triangular waves that converge quite fast.

Almost any waveform is possible, 

including this, 

Okay, so where am I going with this; there is a point here that ties back into population genetics.   Complex curves can be built up from the sum of a series of simpler curves.  However, it is also clear that in some cases the end result can take quite a large sum (the wiggle in the square and sawtooth waves above), in other words the final curve is slow to converge and requires a large number of harmonics.

Kimura's (1955) famous diffusion approximations to model the process of genetic drift in a finite population are built up in a similar fashion.  The final curve is a sum of an infinite series of higher order harmonics.  The math is messy.  It makes use of the hypergeometric function and Gegenbauer polynomials, but the underlying idea is similar to the examples given above.

In the simplest case of the diffusion approximation the series is

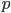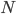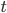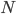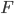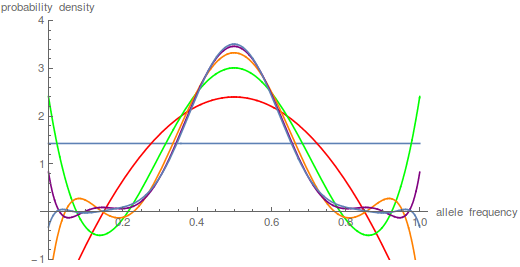
In this equation is the allele frequency, is the population size of diploid individuals, is the time in generations, which is often combined with in a parameter like , and is a hypergeometric function (specifically it is the ordinary Gaussian hypergeometric function ; there are many more but this is the most common).  In the graph below are the first six odd order curves of the series with and .

You can see that they tend to build (are positive) near the centre of the x-axis near a frequency of 0.5 and tend to alternative positive and negative near the edges cancelling each other out for a sum near zero.

Plotting these as sums of each new harmonic plus the previous ones gives these curves.

This plot just focuses on the last step, which is the sum up to in the equation.

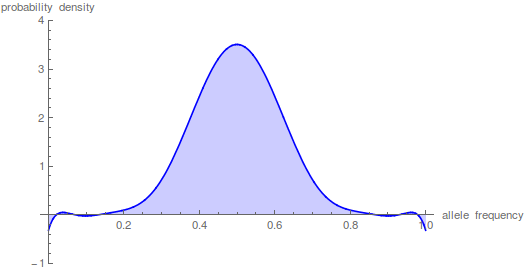
This is starting to give us the expected distribution of allele frequencies expected after N/10 generation of genetic drift when starting from a frequency of 1/2; however, the wiggle to positive and negative values near the edges means that it has not yet converged satisfactory.

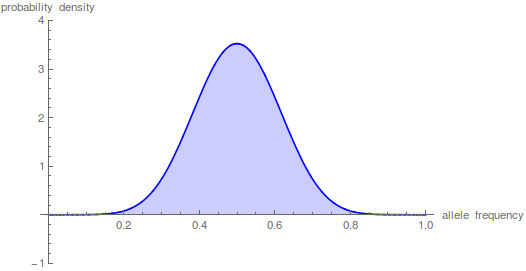
Taking the iterations up to gives a nice result.

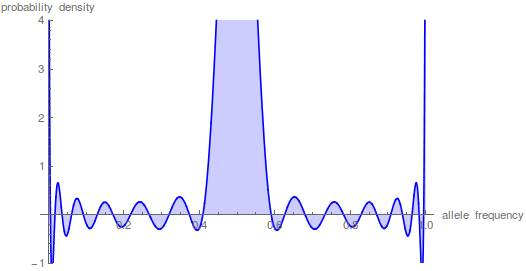
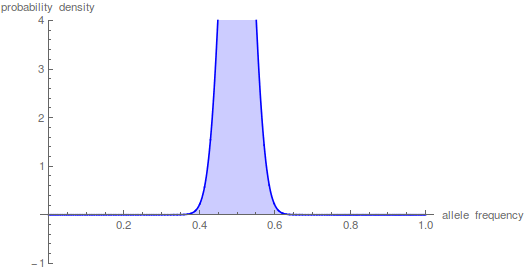
However, what if we want to look at even shorter periods of time.  Holding the y-axis scale the same and letting the peak run off the top of the graph look at what happens after just N/100 generations.

The sum has to be taken up to the to get things to smooth out.

This takes some time on the computer---the hypergeometric function takes a bit of grinding to calculate.  Drift over shorter periods of time is precisely some of the situations where we might want to use this type of approach (it addresses standing variation and ignores new mutations that occur over deeper periods of time). This is why I have been exploring a faster alternative with the beta distribution that I wrote about in an earlier post.

By the way, I used mathematica to generate the plots above.  Here is the code if you are interested.

t = 10;
n = 1000;
p = 0.5;
m = 100;
(*the frequency distribution (probability) of the polymorphic \
fraction*)
poly =
Plot[Sum[p*(1 - p)*i*(i + 1)*(2*i + 1)*
Hypergeometric2F1[1 - i, i + 2, 2, x]*
Hypergeometric2F1[1 - i, i + 2, 2, p]*E^(-t*i*(i + 1)/(4*n)), {i,
1, m}], {x, 0, 1}, PlotRange -> {-1, 4}, Filling -> Axis,
PlotStyle -> Blue,
AxesLabel -> {"allele frequency", "probability density"}]

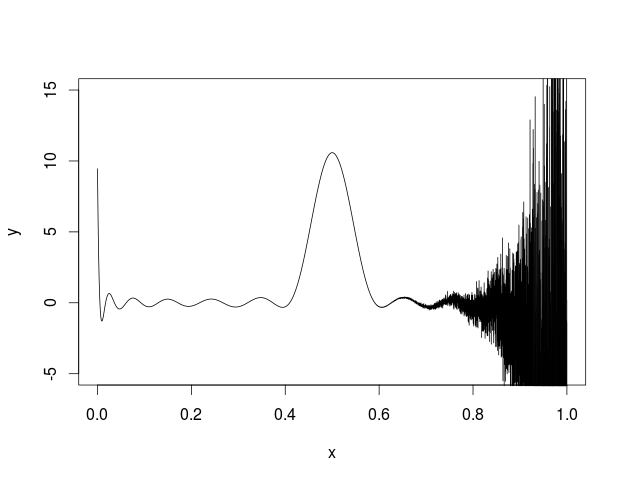
I also tried to plot this in R and got the following.

I'm not sure what is going on but some kind of error seems to be building across the function.

Here is my code
myDiffuse <- function(x,p,t,N,max){
max=25
sum=0
for(i in 1:max){
hypgeosumx=myHypergeoGaussSeries(i,x,max)
hypgeosump=myHypergeoGaussSeries(i,p,max)
sum=sum+p*(1-p)*i*(i+1)*(2*i+1)*hypgeosumx*hypgeosump*exp(-i*(i+1)*t/(4*N))
}
return(sum)
}

myKayAll <- function(i, l){
n=1
for(j in 1:(l-1)){
n=n*(j-i)*(j+1+i)
}
d=factorial(l)*factorial(l-1)
return(n/d)
}

myHypergeoGaussSeries <- function(i, z, m){
h=1
for(j in 2:m){
h=h+myKayAll(i,j)*z^(j-1)
}
return(h)
}

x <- seq(0, 1, len = 10001)
t=10
N=1000
p=0.5
max=5
y<-myDiffuse(x,p,t,N,max)

plot(x,y,type='l',ylim=c(-5, 15))

We had a lab presence at this year's annual Tester Symposium.  Aki Laruson gave the first presentation of the symposium and unofficially won the award for best dressed showing up in an Icelandic linen suit with suede shoes (and he had aviator glasses to top it off) and gave a very good presentation on his current and planned work in sea urchins.  Michael Wallstrom had an awesome poster describing his work with a new invasive algal-associated keratose sponge species.  It gained the notice of Dr. Jeremy Jackson (the invited distinguished guest and keynote speaker) who came over to chat with him about it.

Aki's project has brought some fun elements to the lab that I have not been directly involved in before.  He is sequencing RNA from across the genome from various male and female urchin tissues and needed some larvae to get RNA early in development before the urchins have settled out to the sea floor and are dispersed in the plankton.

So, how do you find microscopic sea urchins larvae in the ocean, much less, how do you know if they are the right species?  It is practically impossible, instead it is simple to make your own---sea urchins are a classic model organism to study early animal development in the lab.  We went out on two different weekends to collect adult urchins and bring them back to the lab.  It tuns out that if you inject them with potassium chloride, or even easier, give them a good shake so they think they are being eaten, they panic and release their gametes.  You can collect them and mix them together.  We also added some heat killed sea water (brought to boiling them back down to room temperature) and took a look at the eggs a day later under a compound microscope.

In the image above are several fertilized eggs at the initial stages of division.  Slightly up and right from the center (about 1 o'clock) is a single undivided cell.  Just down from that near the center is a cell that has divided into two.  In the upper left is an zygote that has divided again into four cells (one is on top of the others, stacked like a tetrahedron).  Moving down from there to the lower left of the image, is a zygote that has divided again into 8 cells.  The initial cell divisions follow a power of two, (where 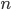is the cell number and 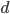is the number of divisions), before the cells become specialized and divisions proceed at different rates.

Below is a closer view of an embryo that has divided into at least 8 cells.  If you look closely you can make out the cell nuclei.  The upper left one is the best defined in the image; it is a smaller circle within the cell.  And there are also hints of sperm flagella in the sea water around the cell (they look like faint lines like individual fibers that are out of focus in various directions).

And below is an embryo that is entering the blastula stage.  The cell nuclei appear slightly more purple in the image.

And a close up at two different focal planes.

In the next  images the cover slip pressed down too hard and the egg coat (egg shell?) has ruptured and spilled out some of the individual cells.  Interestingly, urchins zygotes can loose up to 3/4 of their starting cells and still develop into normal adults.

 

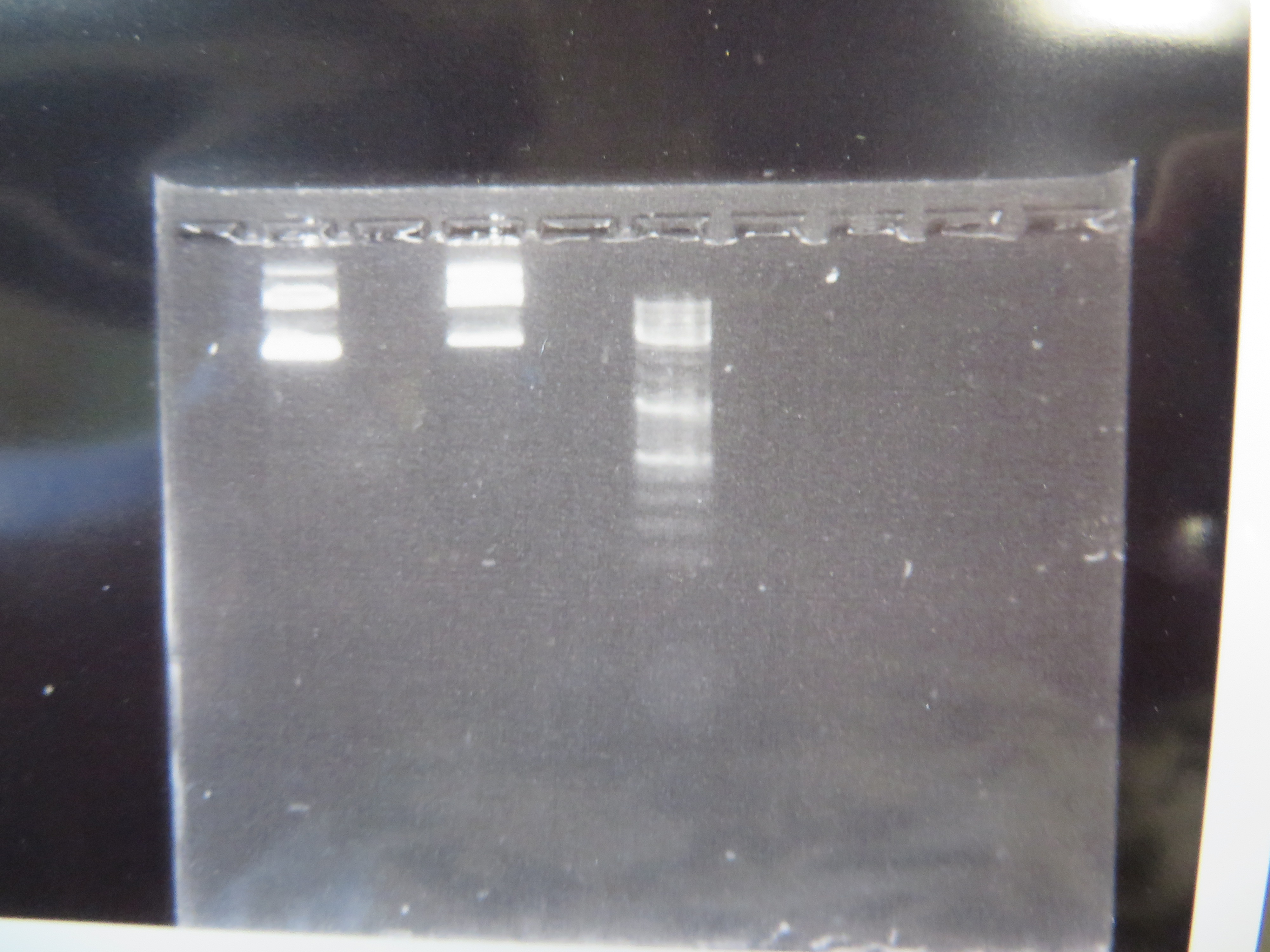
We've taken another big step forward recently.  We are now microinjecting Culex mosquito embryos with genetically modified transposable elements that can potentially integrate into their genome.  We are starting with a test system to save time.  I cloned, grew, and isolated two plasmids (kind of like small artificial chromosomes) in E. coli bacteria that have a piggyBac transposable element system (originally from a species of moth, Trichoplusia ni).  One plasmid (the "helper" plasmid) is immobilized but produces the transposase enzyme that can integrate DNA into the genome.  The other "donor" plasmid is mobile with flanking piggyBac sequences but does not produce its own transposase (Wimmer 2003).  Instead it contains GFP (green fluorescent protein, originally from Aequorea victoria jellyfish) under an artificial 3xP3 "eyeless" promoter that should express in the eyes (which may be occluded by pigments) and larval optic nerve (Sheng et al. 1997; Berghammer et al. 1999).  Here is an image of the two isolated plasmids run on a gel.

The first two lanes to the left show the plasmids and the third lane is a "ladder" to measure sizes.  The lowest band is a supercoiled plasmid.  The higher bands are plasmids that have single strand or double strand breaks in the DNA sequence (and so are less compacted and run slower through the gel).

We loaded the plasmids in the microinjection needle and injected newly laid eggs.  This was a trial run to get the system worked out (injection pressure, egg age timing, slide set up, etc.).  Some of the mosquitoes survived the procedure and were large enough for us to take a good look at them this week under the microscope.  We don't really expect this first batch to contain any genetically modified individuals, although it is possible.  However, even if some cells contained insertions the individual would be a genetic mosaic and may not be transformed in the germ line.  The next generation offspring are the real test.  At this point we are establishing more of a baseline of what the larvae look like.

First of all, here is a larvae under normal light.

We are interested in the pattern of fluorescence under higher energy / bluer light.  This is what they look like in that case.

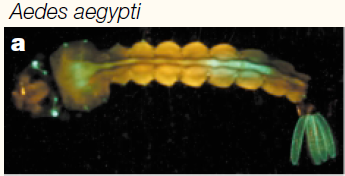
You can see some red and green autofluorescence.  Part of this probably results from the food we give the larvae which shows up as flecks of green and red in the water---the reason to establish this kind of baseline.  Here is the type of pattern (from another mosquito species) behind the eyes (green lines) that we would expect with a 3xP3-EGFP transformation:

In the following images I turned up the regular light a bit so that they are under both light sources.

We will let you know how the next generation turns out...

---

Berghammer, A. J., Klingler, M., & Wimmer, E. A. (1999). Genetic techniques: a universal marker for transgenic insects. Nature, 402(6760), 370-371

Sheng, G., Thouvenot, E., Schmucker, D., Wilson, D. S., & Desplan, C. (1997). Direct regulation of rhodopsin 1 by Pax-6/eyeless in Drosophila: evidence for a conserved function in photoreceptors. Genes & Development, 11(9), 1122-1131.

Wimmer, E. A. (2003). Applications of insect transgenesis. Nature reviews genetics, 4(3), 225-232.