Vox posted an article, "The 7 biggest problems facing science, according to 270 scientists". I would have cast some of it differently and there are some alternative issues I might have focused on but it is worth reading over. It closely mirrors a conversation I had with a grad student last week about struggling to deal with a feeling of cynicism and pessimism in science versus trying to stay positive and focused on research. The section headings are copied below to give you a feeling of what is discussed.
Author Archives: Floyd A. Reed
Can bacteria or parasites take advantage of RNAi against host genomes?
This is an idea I've had floating around in the back of my mind for a few years now. I keep some ideas secret in the short-run because I hope to be able to investigate them some day. However, I also have to face reality, with my teaching load and limited research funding there are a wide range of projects that I simply won't be able to follow up on. I figured it would be better to just put the idea out there so someone can check into this if they want.
RNA interference is a widely used and very useful genetics tool where gene expression can be reduced by double stranded RNA that matches the mRNA of the target gene. There is a great deal of literature on this and I am not going to attempt a summary or review of this technology and its natural role here. Instead I want to focus on a curious fact. For a wide range of species you can simply feed bacteria to the organism that have been modified to express double-stranded RNA and this can create phenotypes by silencing certain genes.
Okay, if this is so easy and straightforward (and quite short sequences of RNA can accomplish this) have any bacteria evolved to take advantage of inactivating genes of a host Eukaryote? Perhaps as a pathogen to block immunity and promote infection, or in a more symbiotic role to tweak host phenotypes? For that matter have any Eukaryotic parasites evolved this ability to excrete dsRNA or antisense RNA to alter host phenotypes? Part of this is a comparative genomics question and if candidate sites are found the follow-up study of activating or inactivating the gene sequence can be done to see if there is a response across species.
Culex Egg Rafts
Culex mosquitoes eggs stick together and are laid in "rafts" that float on the surface of water. In the picture above are four freshly laid egg rafts from our lab mosquito colony, each laid by a single female. They are on the end of a paintbrush that we used to lift them out of the water. They get darker as they age. The two lower rafts are almost the same age; the dark one above them is older and the very light one at the top is less than 1/2 an hour old. To prepare them for microinjection you want to use the very youngest one like the raft at the top. They are seperated from each other and arranged on a glass slide and injected using a microscope and micromanipulator for fine detailed control. They also harden as they age and the light ones can be injected without breaking the thin glass needle that is used. Once they harden you have to use a brief treatment with bleach to remove the out egg surface (chorion) which lowers the rate of survival.
The Square Root of Two
The root of your first period you Must place in quote, if you work true; Whose square from your said period then You must subtract; and to the remain Another period being brought, You must divide as here is taught, By the double of your quote, but see Your unit's place you do leave free; Which place will be supplied by the Square Of your next quoted figure there: Next multiply, subtract, and then Repeat your work unto the end; And if your number be irrational, Add pairs of cyphers for a decimal. - John Hill, 1772, Arithmetick, both in the theory and practice: made plain and easy in all the common and useful rules
This post has nothing to do with genetics or biology, just math. However, I enjoy thinking about math topics from time to time. This is a classic, an example of an irrational number, that goes back to the ancient Greeks. Just to lay it out, the square root of two is an irrational number that is made up of an infinite sequence of non-repeating digits:  . We can prove that it is an irrational number, which have odd properties, and this post is a way to try to better understand this.
. We can prove that it is an irrational number, which have odd properties, and this post is a way to try to better understand this.
The poem above is one method to estimate the square root of a number but an even older algorithm is known as the "Babylonian method." It is very simple and can quickly give reasonably accurate results. 1) Start with a guess of what the square root might be. 2) Divide the original number you are finding the square root of by this guess. 3) Average the resulting number and your guess. 4) Use the average as your new guess and repeat. 5) Stop when you have enough decimal places for the estimate.
To illustrate I will "guess" that the square root of two is one.






In just a couple of steps we have a very accurate estimate of the square root. This was done by the Babylonians 3,700 years ago (link and link). Now let's shift gears and think about tile geometry.
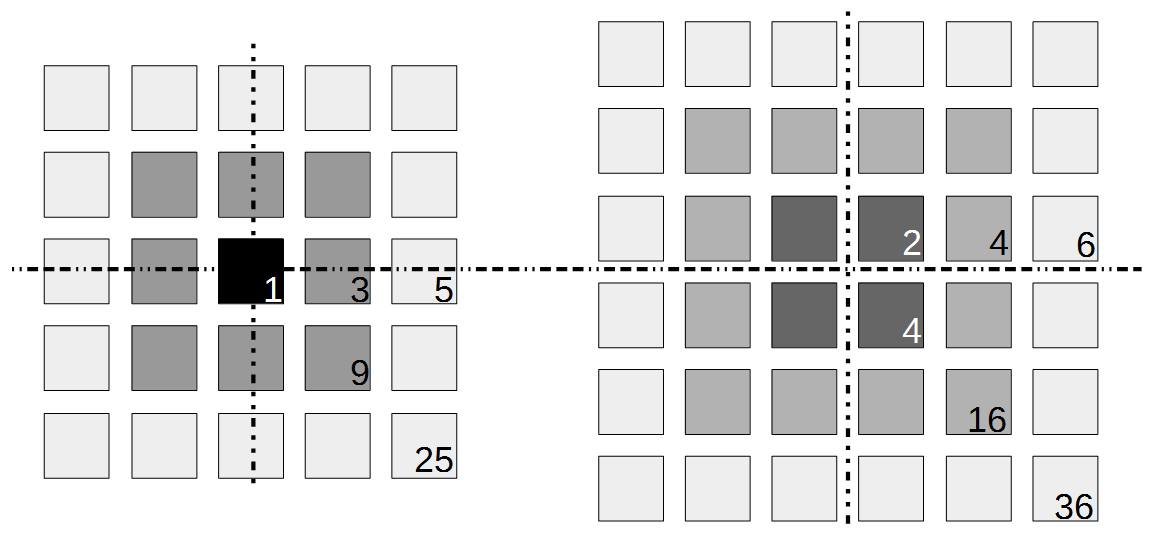
There are two ways to make larger squares out of tiles. You can start with a single tile and add squares around it. Or you can start with zero tiles and add squares around it. Notice that the width of the first kind of square is always an odd number, 1, 3, 5, ... and the width of the second kind of square is always an even number, 0, 2, 4, 6, ... . The square of these numbers are also always odd (1, 9, 25, ...) or even (0, 4, 16, 36, ...). So squaring an odd number always results in an odd number and squaring an even number always results in an even number. You can see this in a kind of visual proof. Evenly folding an odd square together breaks a line of tiles in the middle. However, folding an even square can be done evenly without breaking any tiles. (By the way, the figure contains an optical illusion---the Hermann grid illusion. There are "ghost" dots between the corners of the squares that disappear when you look directly at them.)
Now that we know this rule about the evenness and oddness of tiles in a square we can solve for the square root of two.
Represent the square root of two as a ratio of integers.

Square both sides.

Rearrange.

Realize that since the square of 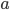 is even (the equation tells us that 2 is a factor of
is even (the equation tells us that 2 is a factor of 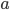 )
) 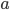 must also be even and can be factored into two and some other number
must also be even and can be factored into two and some other number  .
.

Substitute in the new definition of 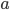 .
.

Solve.

Rearrange.

Simplify.

Realize that since the square of  is even
is even  must also be even and two along with another number
must also be even and two along with another number 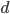 are factors of
are factors of  .
.

Substitute back in.

Cancel out two.

Using the same logic we can show that both  and
and 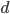 are even numbers, with two as a factor, and this reduction by halves will go on forever.
are even numbers, with two as a factor, and this reduction by halves will go on forever.
A lot of numbers we are used to can be represented by a ratio of integers, e.g.  . And an integer can be factored into a finite set of prime numbers, e.g.
. And an integer can be factored into a finite set of prime numbers, e.g.  . However, the ratio that represents
. However, the ratio that represents  is not the type of number we are used to. Both the numerator and denominator are infinitely large. We can extract an infinite number of factors out of each, 2 being the example here.
is not the type of number we are used to. Both the numerator and denominator are infinitely large. We can extract an infinite number of factors out of each, 2 being the example here.
Another example of an irrational (non-repeated in decimal form) number is  .
. 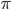 can be approximated by ratios of integers.
can be approximated by ratios of integers.



As the integers in the ratio become larger the approximations become more accurate, they are able to make finer and finer over- or under-corrections to the target, but they will always eventually end up in a repeating sequence because they are integers. To be exactly equal with complete accuracy the ratios that represent an irrational number have to be infinitely large. And we proved above that the numbers that make up the ratio representing the square root of two contain an infinite number of twos multiplied together (among other numbers) and so are infinitely large.
The existence of irrational numbers, that cannot be represented as a ratio of integers, is supposed to have vexed the ancient Greeks with the story of Hippasus. He was supposed to have been killed for his discovery of these strange numbers. And, they get stranger still.
Georg Cantor realized that, while the rational numbers were, essentially by definition, infinite in number, for each rational number there was an infinite number of irrational numbers. So, the number of irrational numbers is infinitely larger than the number of rational numbers, even though both are infinite in number (the number of rational numbers is a countable infinity while the irrational numbers are uncountable).
It may seem strange that there are multiple infinities that are not equal to each other---if it's infinite it's infinite right. Think of the positive integers, 1, 2, 3, 4, etc. there are an infinite number of these. However, for each of these, 3 for example, we could make a set of ratios, 3/1, 3/2, 3/3, 3/4, etc. and there would be an infinite number for each of the infinite integers. The number of integer ratios is infinitely larger than the number of infinite integers, even though there are an infinite number of integers. (However, both of these follow a logical sequence and could in theory be counted if we had infinite time and patience) Now imagine that we wrote out all of the integer ratios, the rational numbers, in decimal form. They will form a repeating structure.
22/7 = 3. 142857 142857 142857 142857 142857 142857 ...
There are an infinite number of positions where the decimal can be changed to break the repeating unit, making it irrational, and this can be done in an infinite number of ways
22/7 ≠ 3. 142887 142857 142157 142857 142857 742857 ...
22/7 ≠ 3. 142857 142857 142857 142857 142857 142337 ...
22/7 ≠ 3. 142857 842857 141856 142857 142857 142856 ...
etc...
There is not necessarily a logical order to go through all possibilities, there are simply too many ways to break up the infinitely long repeating structure, which introduces a new kind of uncountable infinity, even if we had infinite time and patience. So, for each rational number, a ratio of integers, there is an uncountable infinite number of irrational numbers.
Since the number of irrational numbers is so much larger than the rational ones, if we threw a dart at all the the rational and irrational numbers combined we are more likely, with essential certainty, to hit an irrational number at random. Therefore, we shouldn't be surprised that irrational numbers come up so often in mathematics. If it is not tied down to a direct construction from integers (e.g. the sides of a square with the first side set equal to one versus the circumference of a circle, natural logs, golden ratios, square roots of (non-perfect-square) integers) then it almost has to be irrational. In fact isn't it, in a sense, stranger that some things work out so simply like lengths of 3, 4, and 5 can form the sides of a right triangle (another perfect square exception, where two perfect squares (9 and 16) add up to a third perfect square (25), these are Pythagorean triples which are generalized in Fermat's last theorem---that this cannot be done with cubes, etc., and only works for some squares). This suggests that the square roots of numbers are on the edge of being constrained between a direct construction from integers (perfect squares and Pythagorean triples) and the freedom to be any type of number (the square root of all other integers and the irrational side of some right triangles, like 1, 1, and  ). This may be related to being defined in a simpler (and more constrained) two-dimensional geometry since there are no integers that can add up in this way in three or more dimensions (see Fermat's Last Theorem).
). This may be related to being defined in a simpler (and more constrained) two-dimensional geometry since there are no integers that can add up in this way in three or more dimensions (see Fermat's Last Theorem).
There might be a parallel, in a sense, with heterclinic cycles in two-dimensional state space. These are deterministic and seem to be well ordered (they are often asymptotically stable) but the trajectory never moves through the same point twice. It is something that is on the edge of, but not quite, a chaotic system (on the edge of being constrained and the freedom of unpredictably arriving at any value possible); and, for continuous dynamical systems at least three dimensions are required for chaotic behaviors. But I will save that for another post.
DNA Day 2016 and the Structure of DNA
April 25 is an informal "DNA Day" holiday---the date in 1953 when Watson et al., Franklin and Gosling, and Wilkins et al. were published describing the structure of DNA. The Genomics Sections or the Hawai'i Department of Health hosted an event on campus and I, among others, gave a short presentation. I was asked to go over a couple of classes related to genetics in the UH Manoa Department of Biology and to mention a couple of research projects in the lab. A copy of my slides are uploaded here.
I purposely delayed making the slides available as they contained some unpublished data. I am trying to make all of my presentations freely available, but there is some tension in doing this right away when they contain unpublished data. However, Aki Laruson just presented his results at the recent Evolution conference in Austin, Texas; Michael Wallstrom has a paper under revision; and, Gert de Couet and I have a manuscript rapidly getting closer to submission so it felt right to post the slides at this point.
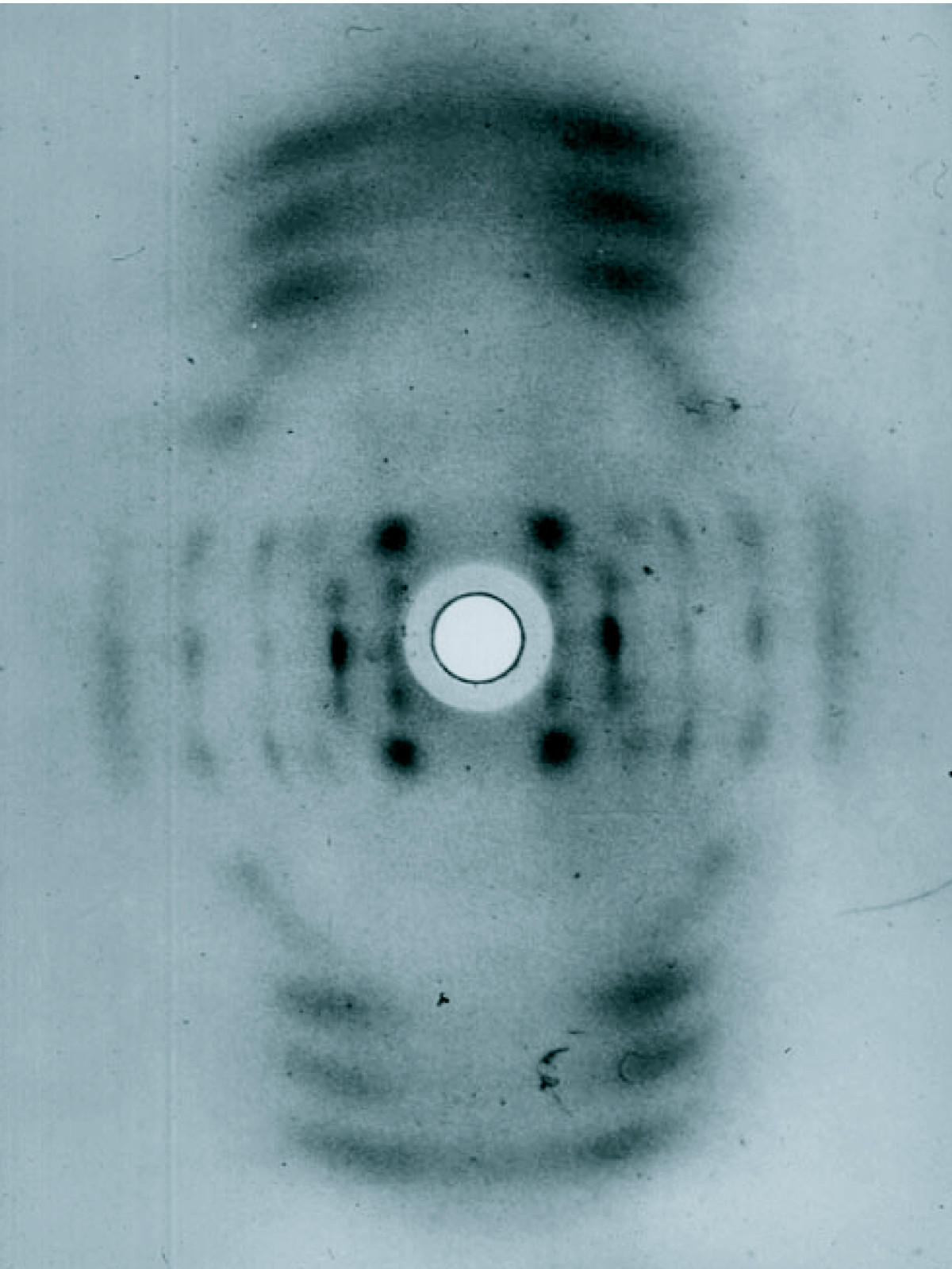
Speaking of the structure of DNA. I like to ask my students in class who made this image below, the first X-ray crystallography of the structure of DNA?
Was it:
A) James Watson
B) Francis Crick
C) Rosalind Franklin
D) Raymond Gosling
E) Maurice Wilkins
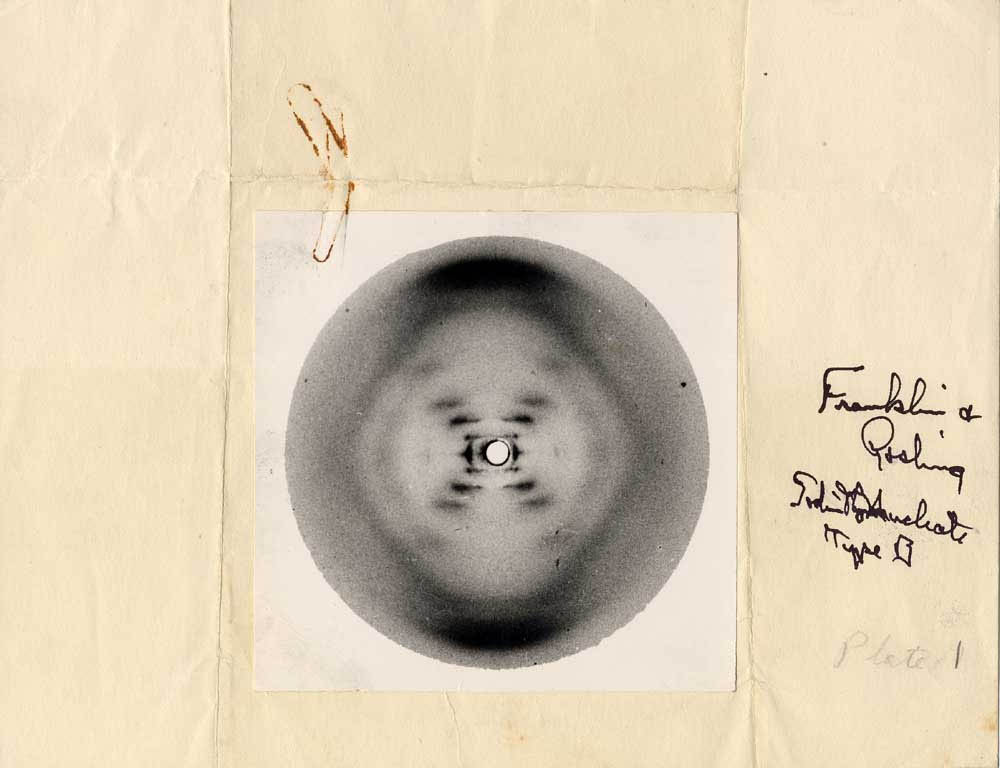
This is a fun question because so many people get it wrong. The story that Rosalind Franklin produced the image that Maurice Wilkins shared with Watson and Crick, and helped them determine the structure of DNA is well known. Most people select C) Rosalind Franklin. And, most people are aware that Watson, Crick, and Wilkins shared the 1962 Nobel Prize for Physiology or Medicine. However, practically no one is aware that Raymond Gosling is the one that actually first made images of DNA structures when he was a graduate student working in John Randall's lab. Later he was reassigned to work with Franklin and they produced the actual image (photograph 51) produced in 1952 that was shared with Watson. Notice the names written on the right side of the paper enclosing the film.
Some accounts give credit for this image to Franklin and some to Gosling. Since Gosling was the one to develop how to crystallize and image DNA, before Franklin arrived, and Gosling was a graduate student working for Franklin, I am fairly certain (unless new contrary evidence comes along) that this was actually made by Gosling.
Further Reading
Wilkins, M. H. F., Stokes, A. R., & Wilson, H. R. (1953). Molecular structure of deoxypentose nucleic acids. Nature, 171(4356), 738-740.
Loki's Castle and the New Tree of Life: Two Domains and the CPR Hidden Folk
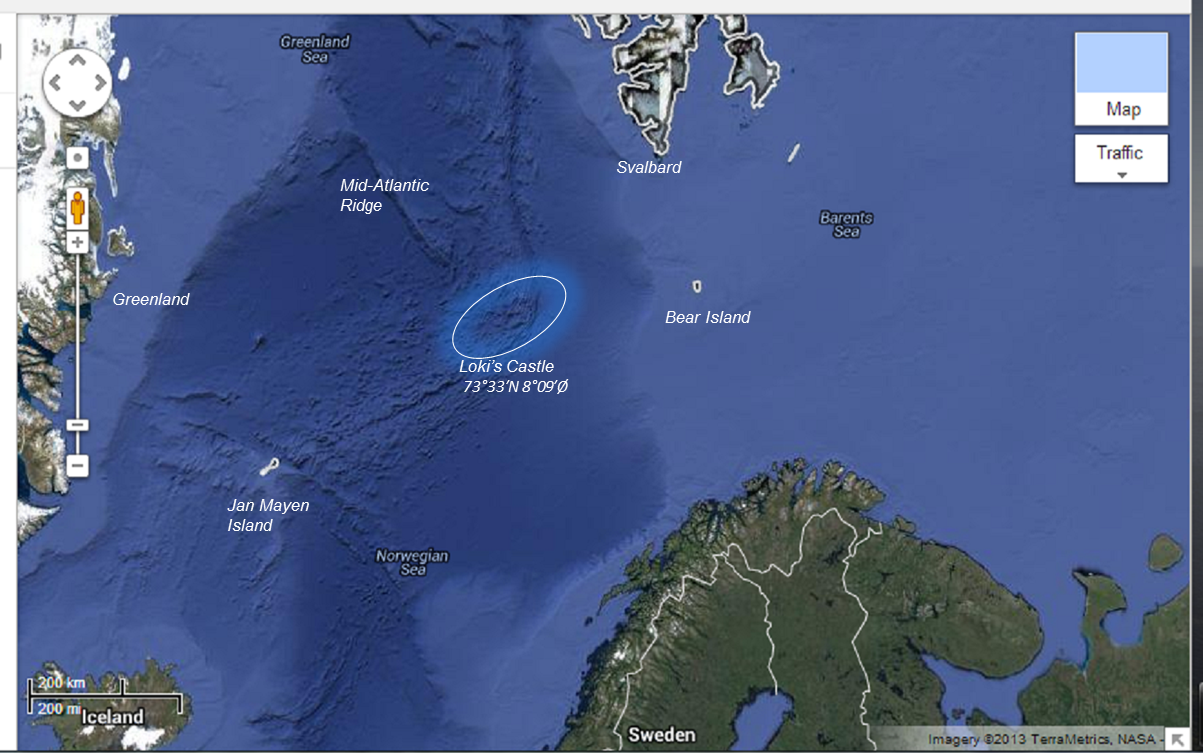
We all know who Loki is (the image above is from the 1700's Icelandic Manuscript, SÁM 66). Today he is seen as a trickster in Norse mythology. Loki had several children and was something like a great-uncle to another god Freyr in the mythological genealogy. Freyr was an ancestor of the Ynglings which was a dynasty of humans. The Ynglings transitioned from mythology to historical figures in the Middle Ages (incidentally one Yngling was Harald Fairhair who violently unified Norway and led to the exodus of families to Iceland, one descendant of which made the image of Loki above) so in a sense Loki's descendants are distant cousins of humans. ...and it turns out that Loki has a castle that was discovered in 2008.
 Loki's Castle is an undersea structure midway between Norway, Greenland, Jan Mayen, and Svalbard.
Loki's Castle is an undersea structure midway between Norway, Greenland, Jan Mayen, and Svalbard.
In 2015 Spang et al. recovered several unusual Archea from the sea floor near Loki's Castle and named them Lokiarchaeota. They share several genetic features with us, the Eukaryotes.
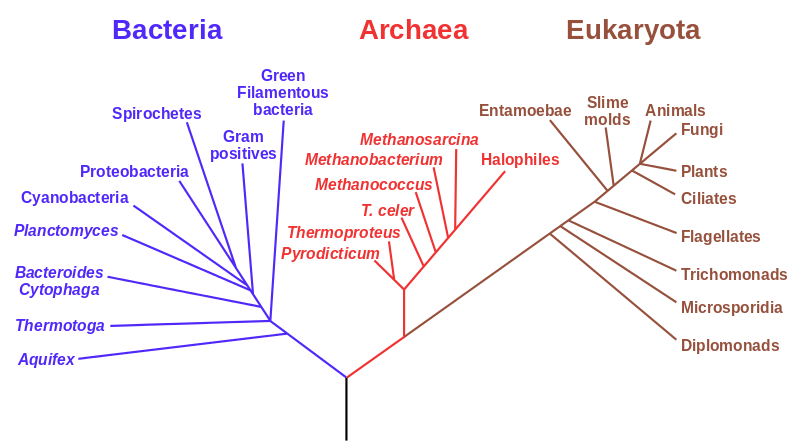
Many of us are now familiar with three domains within the tree of life in the figure above (it is tempting to make another mythological reference here---Tree-of-life---but I have probably already gone to far with the references to Loki and Freyr above): Bacteria, Archaea, and Eukaryota. We are most familiar with multicellular eukaryotes which make up the large forms of life we see around us, animals, plants, fungi. We know about the bacteria which are also common, around us, responsible for some human diseases, and required for healthy ecosystems and digestive tracts. The Archaea are more mysterious. They are single celled microbes that are around but not as abundant as bacteria; they are known for inhabiting extreme environments like high salt concentrations and high temperatures, but are also found in normal environments. In the phylogenetic reconstruction above the Archaea are closer related to Eukaryota than Bacteria but are still a distinct domain of life.
In recent years there have been hints here and there that this picture might be wrong and that the Archaea and Eukaryota are actually even more closely related. When the Lokiarchaeota from Loki's Castle were included in a different kind of phylogenetic tree there was a bit of a surprise.
The Lokiarchaeota are Archaea; however, genetically the "Lokis" are closer related to the Eukaryotes than to other Archaea. In a giant coincidence of taxon naming and mythology (with the right stretch here and there) we are in fact not too distant (within the scale of the tree of life) cousins of the Lokis! And, importantly, this places Eukaryotes within the Archaea; the Eukaryotes are not just related to the Archaea we are directly descended from the Archaea. Eukaryotes have complex cell structures with many types of membranes. The term "eu-karyon" means "true kernel" and refers to the cell nucleus where the chromosomes are stored surrounded by a membrane. There are also mitochondria that are surrounded by their own membranes (and have been secondarily lost in some Eukaryote protists like giardia)---and several other membrane bound organelles exist in Eukaryotic cells. The Lokiarchaeota's "genomes encode an expanded repertoire of eukaryotic signature proteins that are suggestive of sophisticated membrane remodelling capabilities" Spang et al. (2015).
Okay, so now the Eukaryotes are nested within the Arcaea and there are only two domains of life. Are there any other big surprises left?
Well... There have been hints in recent years that a strange group of bacteria exists. Sticking with the theme of this post the idea of a "hidden people" is common around the world's cultures (from Huldufólk Elves in Iceland to Jinn in the Middle East to the Cherokee Nvne'hi and the Menehune here in Hawai'i). These hidden people usually have unusual properties. There seems to be a large part of the tree of life that is widespread and exists, and likely has a large indirect effect on the world around us, but until recently has been completely invisible. And, it turns out that these appear to be very unusual cells.
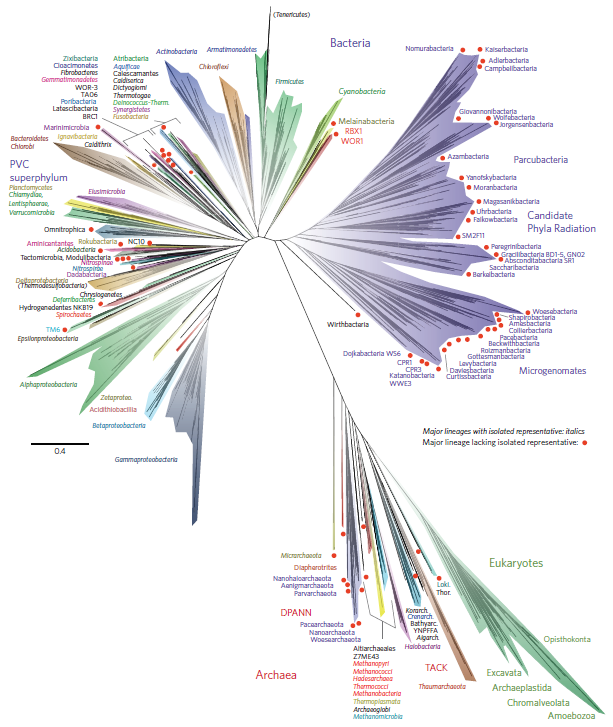
Traditionally in order for new bacteria species to be formally described they need to first be cultured in the lab. However, it is well known that most bacteria that exist in the wild cannot be cultured with standard methods. Capturing DNA from the environment and sequencing it has revealed some strange sequences that appear to belong to bacteria but are very different from any described bacterial phyla---but, many of these mysterious bacteria, while diverse, appear to be closer related to each other than to the known bacteria and this has been referred to as the "Candidate Phyla Radiation" or CPR. Earlier this year Hug et al. attacked this problem head on and made an updated tree of life that includes a large number of these little known and uncultivated mysterious bacteria. A large and diverse sister group to all other bacteria is identified and corresponds to the CPR, adding a deep and diverse branch to the emerging picture of the tree of life.
Hug et al.'s tree confirmed the placement of Eukaryotes within Archaea (lower right) and added a tremendous amount of diversity to the Bacteria with the inclusion of the new CPR (upper right).
What are the CPR bacteria? They are indeed very strange. Brown et al. 2015 studied this in detail. The CPR tend to have greatly reduced genomes and cannot carry out some basic biochemical processes of a free living cell such as the synthesis of nucleotides and amino acids. They also have unusual ribosomal RNA sequences (containing introns and protein coding sequences) that would not have been detected using standard techniques. And, they contain signals that are indicative of parasitic cells that are not capable of living on their own. Taken together this helps to explain why it has not been possible to culture these bacteria independently of other cells. They probably depend upon close association with other cells for many basic molecules of life. An outstanding question is what is their role and importance in natural systems.
As a final note, this is likely not the end of the story. The world of viruses has been left out of this post completely and there are indications of undiscovered groups of highly divergent viruses out there in the environment (e.g. Wu et al. 2011).
Further reading
Brown, C. T., Hug, L. A., Thomas, B. C., Sharon, I., Castelle, C. J., Singh, A., … Banfield, J. F. (2015). Unusual biology across a group comprising more than 15% of domain Bacteria. Nature, 523(7559), 208–211. doi:10.1038/nature14486
Hug, L. A., Baker, B. J., Anantharaman, K., Brown, C. T., Probst, A. J., Castelle, C. J., … Banfield, J. F. (2016). A new view of the tree and life’s diversity, (April), Manuscript submitted for publication. doi:10.1038/nmicrobiol.2016.48
Nelson, W. C., & Stegen, J. C. (2015). The reduced genomes of Parcubacteria (OD1) contain signatures of a symbiotic lifestyle. Frontiers in Microbiology, 6(July), 713. doi:10.3389/fmicb.2015.00713
Spang, A., Saw, J. H., Jørgensen, S. L., Zaremba-Niedzwiedzka, K., Martijn, J., Lind, A. E., … Ettema, T. J. G. (2015). Complex archaea that bridge the gap between prokaryotes and eukaryotes. Nature, 521(7551), 173–179. doi:10.1038/nature14447
Williams, T. a, Foster, P. G., Cox, C. J., & Embley, T. M. (2013). An archaeal origin of eukaryotes supports only two primary domains of life. Nature, 504(7479), 231–6. doi:10.1038/nature12779
Wu, D., Wu, M., Halpern, A., Rusch, D. B., Yooseph, S., Frazier, M., … Eisen, J. A. (2011). Stalking the Fourth Domain in Metagenomic Data : Searching for , Discovering , and Interpreting Novel , Deep Branches in Marker Gene Phylogenetic Trees, 6(3). doi:10.1371/journal.pone.0018011
Further pointers
I am jotting down some more recommendations for pursuing a tenure-track career in biology. I am a sample size of one, and there are other people that can do a much better job than myself in terms of career advice, but I have recently been successful in getting tenure and it doesn't hurt to share some thoughts, especially when they are fresh in my mind. Many things are obvious (publish as much as possible, get teaching experience, apply for funding, maximize a focus on "safer" projects that also have a higher impact in the field and can be done in less time, work in an area that you are naturally motivated in, etc.) so here I am naturally focusing on things that are perhaps less obvious or unnatural (at least to me). And, invariably some people will disagree with me, which is fine; I may be over-correcting on some aspect.
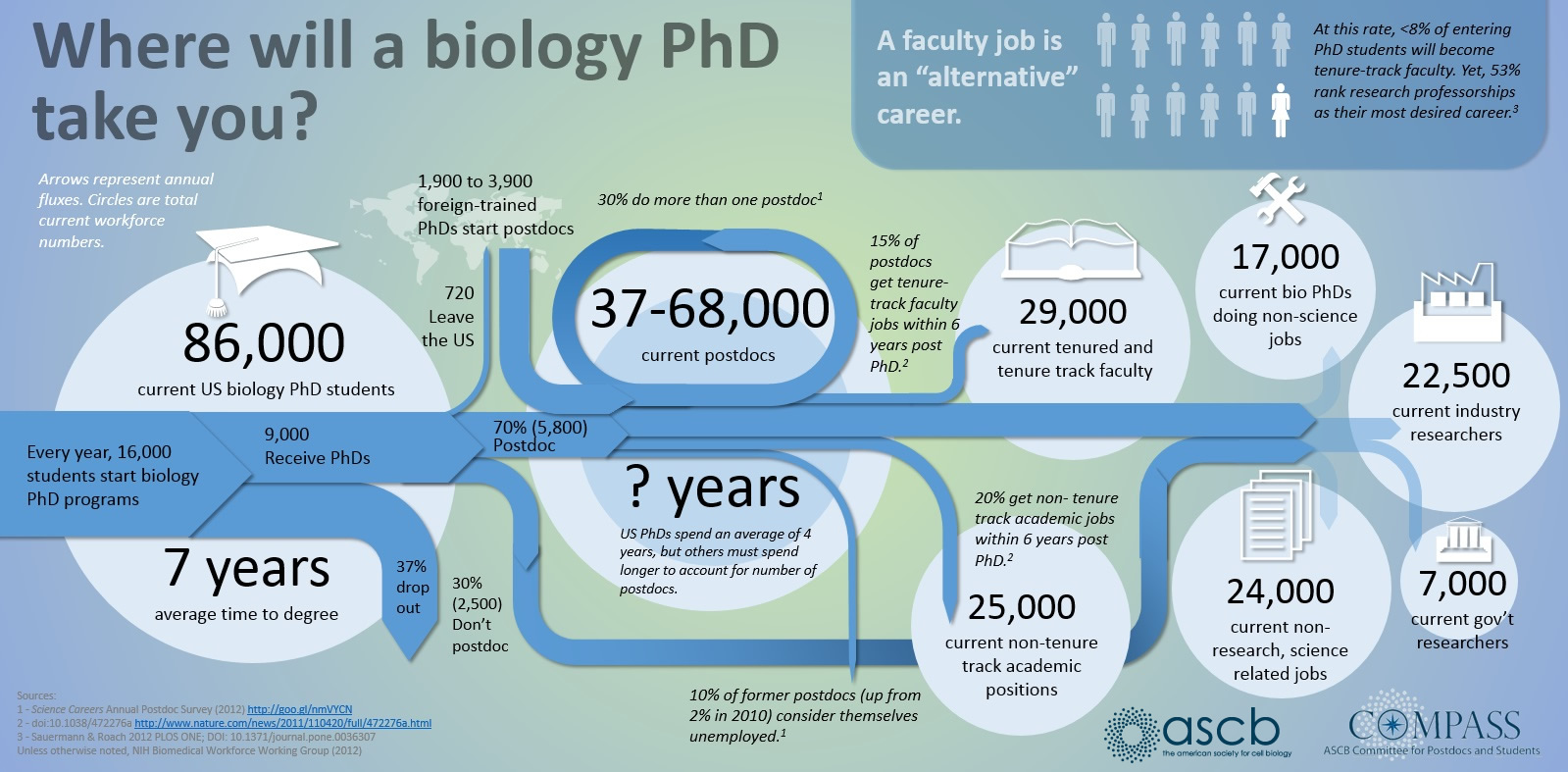
First of all here is a helpful graphic in terms of what to expect (the proportions of people in different positions and time spent in those positions) with a Ph.D. in biology in the US. For example, 10% of the people that start off in a Ph.D. program get a tenure-track position---and obviously less than that, perhaps as many as 8%, get tenure.
1) Networking
One of the things that is much clearer to me in recent years compared to when I started out is the importance of networking and advertising yourself. Something about this goes against my nature; I feel like your work should stand on its own merits or not and you shouldn't resort to tricks like using networks of individuals to get ahead, but it is very important to let people in a field know that you exist and that you are doing cool work. This does not mean only making connections with the established famous people in the field, although that doesn't hurt, but also getting to know a wide range of people in the same position as yourself. Some of these people eventually will be the established famous people in the field and they will be good connections to have. A very important part of this is attending meetings and always accepting invitations to visit other institutions. Remember that every talk is a job talk whether it seems like it or not. Advertising your work will stick in some peoples minds and down the road when they are on hiring/search committees it can affect the kind of research areas that they are looking for and you might even get invited to apply.
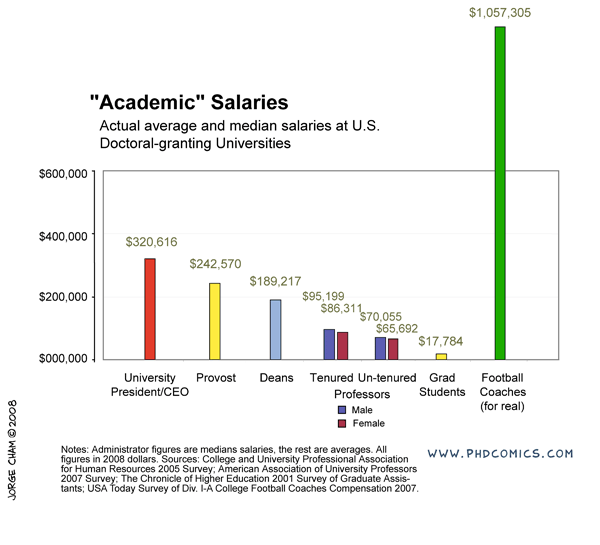
The challenge to this is financial (and take a good look at the levels of support for grad students in the comic above---this is true and not a joke---if your primary goal is a chance to make a lot of money then go into football). It is expensive to travel and to attend meetings. Sometimes you can pay for this off of a grant and sometimes you can get awards to help pay for this, but there is simply not enough support out there to go around and at some point you will have to pay for this yourself, which can be an added challenge if you also have dependents. As an example, I wanted to go to an international meeting in New Zealand. I applied for travel support but was turned down. The lab I was in agreed to cover the air fare (which I truly appreciated, it was a huge help and the majority of the expense) but I still needed more money to pay for a hotel, transportation in NZ, food, etc. I found a temporary night job and did that for a short while (keep in mind, many graduate students are not supposed to work outside jobs as a part of tuition waiver agreements but many secretly do anyway out of necessity) to save up enough for the trip. I attended the meeting and on the return I landed in LAX with exactly $5 left. That was it, no credit on credit cards or money in the bank were available; however, I was getting paid in the next day or two and I was getting picked up from the final airport on the east coast. I was thirsty and had a long layover, so I used it to buy a bottle of orange juice, drank that, and that was it, but I had made it to the meeting in NZ and back.
2) Establish yourself in a "narrow" field
Another factor that is much clearer to me now than it was years ago is the importance of staying within a defined area. Funding agencies, journal editors, and almost everyone in science say how important interdisciplinary work is---but don't fall for it too early in your career. It may in fact be important but unfortunately it is not what gets funding and gets published. This is another factor that goes against some part of my basic nature; I am curious about a wide range of subjects and enjoy thinking about very different projects. However, this has greatly slowed down my career advancement. I have changed fields from a Drosophila lab studying the effects of natural selection to human genetics studying gene-culture coevolution to designing gene-drive systems in insects AND natural history and evolution in the Indo-Pacific. A common theme throughout all of this is population genetics but this is too broad. Each time I switch to a new field I have to work to become "known" to people working in the field and this is an added challenge in getting grant funding and publications. It is well known that there is a very strong "Matthew Effect"[1] in science; there is a circular positive feedback where the people that are successful in a field become even more successful in a field simply because they are successful in the field (because funding is limited this has the counter negative feedback where people that are not well known cannot get established; also, a lot of success within a field is inherited from advisors). This has led to occasionally comical interactions where other scientists have "explained" published research to me that I actually carried out and published; they just forgot and/or didn't expect me to be the author of the article that they read. One of the coolest projects I have been involved in was literally drawn on a napkin over lunch; I drew out an experimental economics "game" that occurred to me. One of the other scientist at the table (who did this type of research) carried it out in his lab over the following months; we wrote it up and eventually it was published in PNAS; which was not bad. Later I had people ask me why I was an author on the manuscript despite---unknown to them---coming up with the idea, analyzing some of the results, and writing part of the manuscript, because they had pigeon-holed me and didn't expect that I could have anything to offer to an experimental economics project. I wish that science could be more truly interdisciplinary, but unfortunately, frankly, it will not help you to become established in your career. Rather, you should stay within what may seem like a painfully narrowly defined area and be incremental, changing just one or two aspects of your research at a time between projects (same question with a different method or same method with a different species/question, etc.). Either explore diverse areas very early, preferably as an undergrad or grad student, or wait until you are well established to broaden your active interests back out, do not do this as a postdoc or assistant professor---or if you are like me you will just ignore this advice anyway.
3) Honest advice on your CV
Find people that can give you feedback on your CV. Most importantly people that are not afraid to criticize you. Your CV is the most important record of your advancement in the field and you have to focus on developing it. Use someone else's as a template and copy its format. I obsessively updated mine every time I had a new publication or presentation. Also, don't be afraid to create new categories like "media impact" or "service to the field" and unashamedly brag on yourself; this is one of the places where it is appropriate and expected. (And, bragging on myself is another thing that I still working to overcome; I guess it is related to the culture I was raised in; however, modesty and humility are not rewarded in science.) I have relied on a few people over the years that were not advisors in any official sense and they have helped me tremendously, giving me pointers like I needed more publications or presentations and not to worry so much about grants, etc., at such and such a stage. Having mentoring advice, which is on you to seek out and establish a mentor relationship, is extremely important for people that are the first in their family to go into academia, without the family advice that some people benefit from.
4) Avoid moving between systems
This hurts me to say, but avoid moving internationally if possible. Unless you are a super-star where no matter what you do it will be seen as a plus (see Matthew effect[1]), moving between systems will only count against you. Here is my experience in this respect. After completing a Ph.D. in grad school I did a postdoc at the University of Maryland. I was working in human genetics with a focus on Africa. I had significant college loans that I was paying back and I applied for a competitive NIH loan repayment program for people working in health disparities research, with a catch that you have to remain working within academia for a certain period. All along I communicated with the NIH office that I was actively applying for my next academic position and would be changing institutions, and they told me that this was not a problem just to update the information with them once I moved (they never once told me that I could only move within the US; academia is very international; it is common to have a diverse range of nationalities working together within a lab).
I applied widely to many different job opportunities and finally landed a position as an "independent group leader" at a Max Planck Institute in Germany that was advertised as equivalent to an assistant professor position in the US (in this position I had my own lab, funding, independent research, applied for grants, taught classes, had students and postdocs, served on committees, etc.). In this new position I started a completely new line of research that was independent from my work in graduate school and independent from my postdoctoral work. I notified NIH of my new address and position and things immediately got weird. Suddenly there was a problem, since I was now employed in academia outside of the US (what choice did I have? this was the only job offer I had within academia, which is one of their requirements). Apparently, I was in violation of a rule that they had neglected to communicate to me, despite my communication with them that I was changing institutions in the near future. Apparently you are not allowed to work outside of the US or you can be fined. They threatened me with this fine, which was larger than the total amount I had in college loans in the first place. After some back and forth communicating they finally "forgave" me and I was kicked out of the repayment program after it had just started. Okay, so I had wasted a significant amount of time applying for this (when I could have been writing grant applications and manuscripts for publication) but compared to what they could have done to me I had dodged a bullet.
Jumping ahead, after working in Germany for a few years I applied for a new position and landed a tenure track job here at UH. However, my work in Germany was not counted as the equivalent of experience in an assistant professor position. I could not apply for tenure and promotion early based, partially, on this prior position. Some of the faculty in my new department referred to my work in Germany as a postdoc position (despite my corrections, I hired my own postdocs in Germany). They also insisted that many of my publications were "meaningless" for tenure because they were related to work that I had done in my previous lab in Germany (I guess they were thinking this work was done under a "postdoc advisor" ?). People construct scenarios that fit their expectations and it is difficult and tedious to try to change their minds. Also, my current graduate student in Germany could not move to my new lab because of visa/citizenship issues in her family. I was contacted by people wanting to work in my lab---in Germany---but they were not willing to move around the world and I was not known in Hawai'i and the West Coast. Essentially, my time in Germany establishing a new lab did not count and I had to start completely over.
But, I couldn't start over. I had received a federal grant from the DFG in Germany. Once you receive a federal grant as a PI you loose "young investigator" status with NSF (I talked with an NSF officer who confirmed this), which put me at a relative disadvantage to other new assistant professors...at the same time this DFG federal grant did not count towards tenure in my new position at UH. Also, I had been in labs, and helped write applications, that were funded by NIH. In Germany I learned how to apply to the DFG. Now I had to break into the NSF funding world with all of the unspoken rules, red flags, weird definitions, and key words that they were looking for (NSF "Broader Impacts" are very unusual compared to other funding agencies and are very strictly defined---e.g., I was criticized by reviewers for including broader impacts that were economic rather than strictly educational).
In an ideal world we could live and work internationally. I think this is something that should be encouraged, especially in science. However, in my experience it only counts against, and is turned against, you (people in power look for excuses to fit you into, or not fit you into, a particular category depending on their motivations, having an unusual background provides enough ambiguity to be flexible about this). Like the interdisciplinary advice above, either do this very early or wait until you are well established to make an international move.
5) Nepotism
I'm not sure that this is really advice but it is a non-obvious aspect of a career in science that is worth sharing. This is something that seems to be unique to academia (within the US). When you are hired to a faculty position there is a possibility of a "spousal hire." In other words finding a position for your spouse within the university. However, your spouse also has to be in academia with the credentials to be hired as a faculty member in a department. If your spouse works outside of academia or, as in my case, has had to delay their career advancement in order for you to advance (we could not afford to simultaneously attend graduate school, however, my wife has a psychology degree and experience working in academia both in research labs and as department support staff, but does not qualify to be hired at the tenure-track faculty level) this opportunity is not extended to you.
This is a very weird situation. I didn't even realize it was legal for institutions to openly embrace it when I started out in academia. It is brought on by how rare positions are within a specific research field, so that it is practically impossible for faculty-track couples that meet later in life (grad school or after) to be hired within their career in the same geographic location. However, it is obviously nepotism (not that there aren't some excellent people in science that are also spousal hires) and puts couples that have been married for longer and met earlier in their careers (and do not have family resources to help pay for an education) at a relative disadvantage.
6) Dealing with disabilities
We all have different challenges that we have to work to overcome. Here I can only speak from my own perspective but I intend this as a general statement. Like approximately 5% of the population I am dyslexic. I am very slow at reading and writing compared to most people, having to frequently reread sentences as I go; I also don't passively read text around me (like posted signs). This makes it a challenge to keep up with current literature and especially email (tricks like black or dark gray text on a yellow background help). I am also a horrible speller; I still have to look up the difference between discreet and discrete. I have had assess go wrong more than once in a manuscript and recently accidentally used salacious for siliceous (a different underline color should be used in text editors for words that are spelled correctly but can easily be the wrong word). This means that I simply have to dedicate more time in my schedule to reading and writing.
I am also partially deaf with a complete loss of hearing in one ear and some hearing loss in the other. One of the results of being monaural is that I cannot separate voices from background sounds, something that most people are able to do instinctively and cannot truly understand without experiencing it (plugging one ear is not the same, I do not have bone conduction of sounds which people with normal hearing still have and can use subconsciously to pick up on auditory cues). This is a social handicap but at the same time it is cryptic. I can hear people and understand them (I am also able to use lip reading to a certain extent) but in situations where there is significant background noise, especially when it is other human speech, it becomes very difficult to filter out what someone is saying---and repeatedly explaining this becomes both burdensome and prone to misinterpretation (imagine saying at a scientific meeting "I'm sorry but I can't understand what you're saying..." without time to explain). My wife and I have worked out some of our own hand signs to use in situations where I cannot hear, but this doesn't work for other people. Above I talked about how important it is to network and attend meetings; however, during the social parts of these meetings, where many people are talking together in a room, I cannot effectively communicate with other people, which can easily give the wrong impression. Also, during presentations when I am in the audience and there are questions from the audience I often cannot hear what people are asking because I cannot see their face while they are talking---this leads me to not saying anything because I am worried that I might repeat a question or comment that everyone else heard. Fortunately there are ways to address this. It is not easy but situations can be engineered where you can talk to people one-on-one or in a small group in a quiet area, "hey, let's get some lunch," or "coffee," etc. (Although, talking while eating leads to some people covering their mouth with their hand, which is a problem for lip readers.) Also, I have run into a surprising number of people just after a meeting at the airport, where they tend to be alone with unplanned time and it is a perfect opportunity to introduce yourself and have a conversation---I actively scan for these people now. I have run into a few (I can count on one hand) people that are also monaural in science. The specifics of this section are obviously not general advice, but the strategy, engineering or taking advantage of opportunities to overcome an issue, is what is intended.
1) 'In the sociology of science, "Matthew effect" was a term coined by Robert K. Merton to describe how, among other things, eminent scientists will often get more credit than a comparatively unknown researcher, even if their work is similar; it also means that credit will usually be given to researchers who are already famous. ... Merton furthermore argued that in the scientific community the Matthew effect reaches beyond simple reputation to influence the wider communication system, playing a part in social selection processes and resulting in a concentration of resources and talent.'
https://en.wikipedia.org/wiki/Matthew_effect#Sociology_of_science
Undergraduate Showcase
I am still catching up on old posts from earlier in the semester.
On May 6th Michael Wallstrom and Zhaotong Xu presented their research at the "Undergraduate Showcase". This is held at the end of each semester at UH Manoa for undergrads to present research they have conducted.
Zhao worked on the cellular/developmental effects of PRAF2 ectopic expression in Drosophila and Michael worked on the phylogenetics and morphological description of a new Porifera species.
Richard G. Harrison
I (Floyd Reed) just learned that Rick Harrison passed away in April while on vacation in Australia. I came across a nice memorial article to him in the latest edition of Molecular Ecology. I did my first laboratory rotation in his lab when I first arrived in graduate school in the fall of 1996. After years of only reading and thinking about PCR I was able to set up my first PCR reaction in his lab in an RFLP project with gypsy moth (Lymantria dispar) samples from around the world (to try to identify the source of introduced populations). Later he became a member of my Ph.D. committee (for my Ecology and Evolution minor, the program I was in had Ph.D. minors). I still remember some of the other people in the lab; Steve Bogdanowicz (who first taught me a lot of molecular genetics lab skills), Chris Willett who is now at UNC Chapel Hill, Matt Hahn was an undergrad doing an experiment on copepods from lake sediments, and Mohamed Noor a postdoc in Chip Aquadro's lab collaborated with Rick on a cricket experiment. There were a few other people around the lab but I can't quite remember there names just now. One postdoc was working on generating a recombinant genetic map in beetles and later moved to Maryland, another grad student was working on a flying fish phylogeny... And of course there was the ram's skull with giant horns over the door to the darkroom where gels were visualized with UV.
Rick was a cheerful, intelligent man that was sometimes intimidating (to a new graduate student) but I did value and enjoy talking with him. He was very available, had a sense of humor (once he brought in some coprolites and asked the students to identify them), and seemed to have an endless supply of energy. He was interested in a wide range of subjects---I remember one conversation in particular about how broad versus how focused one should be on research subjects in the development of a career.
He is the second member of my graduate committee to pass away. Ken Kennedy (Physical Anthropology minor) passed away in 2014. It is hard to think that they are no longer with us.
Mutation-Selection Equilibrium
How do you permanently increase or decrease the fitness of a population (in terms of population genetics). Is it better to intensify the strength of selection so that deleterious mutations are removed, or relax the strength of selection so that mutations are better tolerated. This is something that is relevant to the current human condition, where there is an increased amount of medical intervention and (in the very recent past) a relaxation of some adaptive demands in the environment (this will be misunderstood, human culture has placed additional demands upon humans in the longer timescale, but anyway...). Arguments can be made for either scenario and---it turns out that it really doesn't matter. Strangely enough the strength of selection cannot change the average fitness (at equilibrium) of a population.
For this post only think of mutations as deleterious (they lower an organism's fitness) if they have any effect at all. Most mutations either have no fitness effect (are selectively neutral) or lower fitness. Very few mutations in the genome would actually increase the fitness of an organism (adaptive). Again think about making random changes to a car. Most changes, slightly reducing the length of the radio antenna, either make essentially no difference or, reroute the fuel line to the windshield wiper pump, are a very bad idea in terms of performance of the car. It would be very rare to make random changes that increase the performance of the car.
So, we know there are deleterious mutations that exist in a population that can result in what we identify in humans as a genetic disease. Many of these are recessive such as cystic fibrosis or Tay-Sachs disease; however, some are dominant such as Huntington's disease or Marfan's syndrome. And some do not fit this simple category such as X-linked hemophilia. Why do human and other species have so many deleterious alleles in the population?
The alleles are generated by mutation and removed by selection. We can have a mutation rate 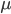 and a strength of selection (relative to unmutated alleles) acting on those mutations
and a strength of selection (relative to unmutated alleles) acting on those mutations 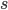 . If we pretended the alleles acted independently, that pairing them together into diploid genotypes did not matter, then we can easily write down the equilibrium allele frequency,
. If we pretended the alleles acted independently, that pairing them together into diploid genotypes did not matter, then we can easily write down the equilibrium allele frequency, 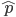 , of the mutation.
, of the mutation.
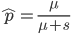
This is the rate that the allele is generated, 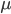 , out of the total rate of input by mutation and removal by selection. For example, if the strength of selection against a mutant is 20% (a 20% fitness reduction relative to individuals with unmutated alleles) and the mutation rate is 0.1% then the equilibrium allele frequency is approximately one half of a percent, 0.5%. On the other hand if the fitness reduction is only 1% the allele can reach a higher frequency in the population at the same mutation rate (
, out of the total rate of input by mutation and removal by selection. For example, if the strength of selection against a mutant is 20% (a 20% fitness reduction relative to individuals with unmutated alleles) and the mutation rate is 0.1% then the equilibrium allele frequency is approximately one half of a percent, 0.5%. On the other hand if the fitness reduction is only 1% the allele can reach a higher frequency in the population at the same mutation rate (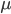 =0.1%) the equilibrium becomes approximately 9%, which is a dramatically high frequency for a dominant deleterious allele. (This is mathematically equivalent to bi-directional mutation; however, here the "back mutation" to restore the original state is selection.)
=0.1%) the equilibrium becomes approximately 9%, which is a dramatically high frequency for a dominant deleterious allele. (This is mathematically equivalent to bi-directional mutation; however, here the "back mutation" to restore the original state is selection.)
Now lets keep track of genotypes and the case where the fitness effect of the allele is dominant (with some simplifying assumptions). If it is dominant and deleterious it is probably rare (not like the 9% case above), so homozygotes, 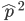 are exceedingly rare and can be safely ignored because they contribute very little to the equilibrium dynamics. Mutations occur on the non-mutant allele copies
are exceedingly rare and can be safely ignored because they contribute very little to the equilibrium dynamics. Mutations occur on the non-mutant allele copies 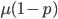 (regardless if they are present in a homozygote or heterozygote). Selection removes a portion of heterozygotes, according to Hardy-Weinberg heterozygotes are expected to appear at a frequency of
(regardless if they are present in a homozygote or heterozygote). Selection removes a portion of heterozygotes, according to Hardy-Weinberg heterozygotes are expected to appear at a frequency of 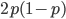 and an
and an 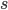 fraction of these are removed so the genotype rate of removal is
fraction of these are removed so the genotype rate of removal is 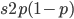 .
.
(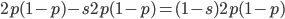 , the relative fitness to the unmutated homozygote is
, the relative fitness to the unmutated homozygote is  which adjusts the frequency of the heterozygotes
which adjusts the frequency of the heterozygotes 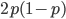 due to selection.)
due to selection.)
Only half of the alleles in the heterozygotes are the mutant allele so the rate of removal of the mutant allele is 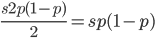 . (Here we are focused on the case where the mutant allele is rare, which allows us to ignore
. (Here we are focused on the case where the mutant allele is rare, which allows us to ignore 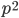 in the first place. So,
in the first place. So, 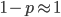 . The frequency of heterozygotes is then approximately
. The frequency of heterozygotes is then approximately 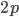 . However, we want to keep track of the change in
. However, we want to keep track of the change in 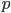 due to
due to 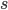 so we divide
so we divide 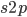 by 2. Selection is also removing non-mutant alleles in heterozygotes but the non-mutant homozygotes are much more common so we just ignore the other half of the alleles that are removed due to selection; this comes from the assumptions of large population size and rare mutant allele frequency.)
by 2. Selection is also removing non-mutant alleles in heterozygotes but the non-mutant homozygotes are much more common so we just ignore the other half of the alleles that are removed due to selection; this comes from the assumptions of large population size and rare mutant allele frequency.)
At equilibrium the rate of input and removal of the mutation are equal.
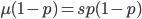
Rearrange and simplify.
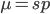
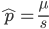
Using the two examples above with a mutation rate of 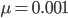 the equilibrium allele frequency is predicted to be 0.5% for a fitness reduction of 20% and 10% for a fitness reduction of 1%, which is almost equivalent to the case where alleles are acted on independently (as haploids). (If
the equilibrium allele frequency is predicted to be 0.5% for a fitness reduction of 20% and 10% for a fitness reduction of 1%, which is almost equivalent to the case where alleles are acted on independently (as haploids). (If  then
then 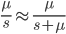 .)
.)
What if the fitness effect is recessive? Then selection only removes the mutant homozygotes which are predicted to occur at a frequency of 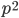 . In this case selection can proceed more efficiently, in a sense, and mutant alleles are removed in pairs. All of the alleles in the homozygote are the mutant form so there is no adjustment necessary like dividing by two in the heterozygotes.
. In this case selection can proceed more efficiently, in a sense, and mutant alleles are removed in pairs. All of the alleles in the homozygote are the mutant form so there is no adjustment necessary like dividing by two in the heterozygotes.
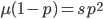
To keep this from getting messy let's use the 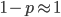 trick now (which is actually less appropriate in this case because higher frequencies can be attained, but for now still assume that mutant alleles are very rare,
trick now (which is actually less appropriate in this case because higher frequencies can be attained, but for now still assume that mutant alleles are very rare,  , which is true for many mutations that result in human genetic diseases).
, which is true for many mutations that result in human genetic diseases).
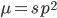
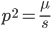
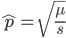
Using our two examples again, with a mutation rate of 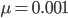 the equilibrium allele frequency is predicted to be 7% for a fitness reduction of 20% and 32% for a fitness reduction of 1%. Now the equilibrium allele frequencies are much higher, when very rare (when
the equilibrium allele frequency is predicted to be 7% for a fitness reduction of 20% and 32% for a fitness reduction of 1%. Now the equilibrium allele frequencies are much higher, when very rare (when  ) the difference can be many orders of magnitude. Masking the fitness effects in heterozygotes (carriers) allows the allele to get to unexpectedly high equilibrium frequencies.
) the difference can be many orders of magnitude. Masking the fitness effects in heterozygotes (carriers) allows the allele to get to unexpectedly high equilibrium frequencies.
Now let's look at the average effect in the population. The average fitness 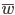 in a population can be calculated as the fitness of each genotype multiplied by its corresponding frequency. Let's say the fitness of unmutated homozygotes is 100% or 1. In the case of a dominant fitness effect
in a population can be calculated as the fitness of each genotype multiplied by its corresponding frequency. Let's say the fitness of unmutated homozygotes is 100% or 1. In the case of a dominant fitness effect
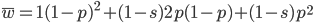
Expand and simplify
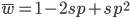
Let's say 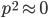
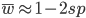
Substituting in 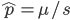
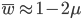
The average fitness is one minus twice the mutation rate.
On the other hand if selection is recessive
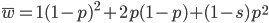
Expand and simplify
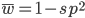
Substituting in 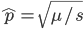
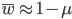
The average fitness is one minus the mutation rate.
Interestingly, the average fitness in the population does not depend on the fitness of the genotypes within the population; it is only a function of the mutation rate! (However, it does depend on the type of dominance; recessive deleterious effects result in both a higher equilibrium allele frequency and a higher average fitness.) This seems like a paradox at first. In our examples from above, if selection is dominant, then with a mutation rate of 0.1% the average fitness within the population is 99.8% regardless of how strong selection is against the mutation. If the mutation is recessive the average fitness is actually higher 99.9%, again regardless of the strength of selection against the mutation (this is related to selection being more efficient when it acts upon pairs of mutant alleles rather than one at a time in heterozygotes).
Why is average fitness only determined by the mutation rate? The trick to understand this is to realize that the strength of selection against a mutation and the frequency of the mutation in the population at equilibrium cancel out in terms of the average effect in the population. A mutation with a strong effect can only exist at a low frequency and only affect a few individuals, while a mutation with a weak effect attains a higher frequency and affects more individuals. The average effect of these two mutations, that have very different effects on fitness, in a population at equilibrium is the same.
However, going back to the original question of this post, changing the mutation rate can permanently change the average fitness of a population. How do you change the mutation rate? Well certain chemicals and radiation are well known examples. (Also, in a recent article Michael Lynch points out that if relaxed selection affects mutations in genes that affect the mutation rate itself, DNA repair, etc., then there could be a feedback effect where selection does influence equilibrium average fitness by altering the mutation rate.)
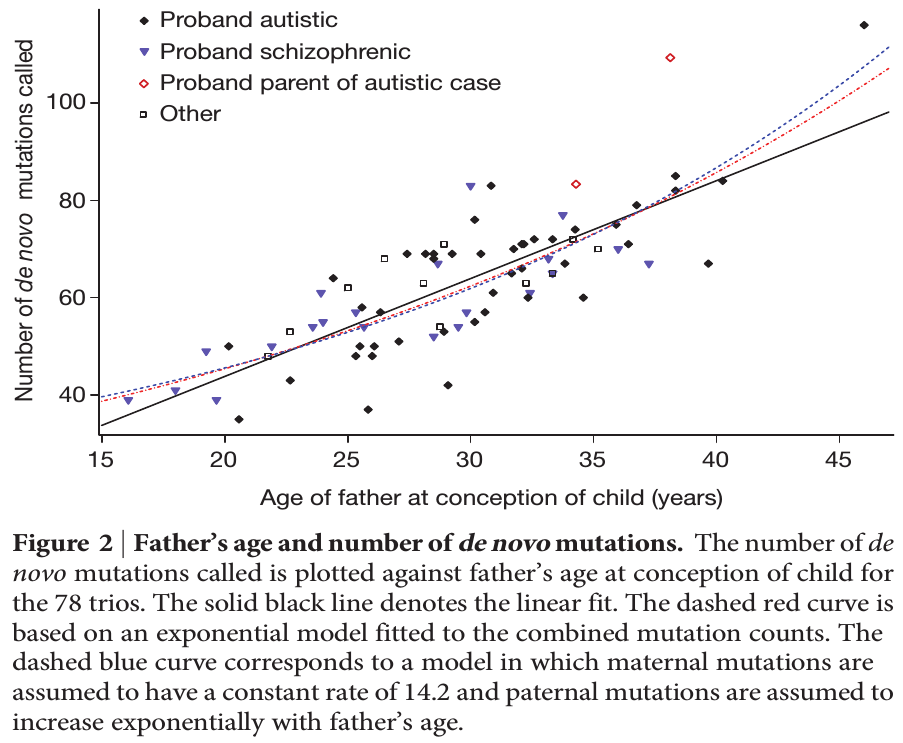
To put this in perspective, mutations are not rare unusual events that can safely be ignored; they affect all of us. We all have new mutations that can be passed on to our children. Whole genome sequencing estimates this as high as to be around 40-80 new mutations depending on the age of our father. (Click on the image below for the source information.)
Each year of father's age adds on average two new mutations. The age of the father is also a risk factor for diseases like autism and schizophrenia and new mutations might be playing a role.
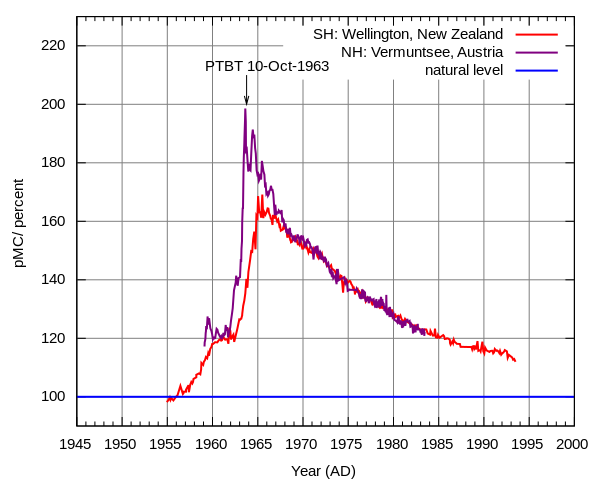
Above ground nuclear testing released large amounts of radioactive particles into Earth's atmosphere which spread planet-wide. At the height of the Cold War before the 1963 partial test ban the amount of radiation in the atmosphere was almost doubled (click on the image for a link to more information about how it was generated).
This had very real effects, for example it created a market for pre-war steel for specialized equipment like Geiger counters to test levels of radiation (steel made after WWII was contaminated with atmospheric radiation). A particularly valuable source are WWI battleship wrecks that are protected under water from contact with the atmosphere.
The increase in radiation alarmed some population geneticists like Hermann Muller who studied mutations and their effects on fitness. He helped raise awareness of the issue and his work among others contributed to the partial test ban treaty.
Furthermore, we come into contact with a wide range of industrial chemicals, many of which are seriously toxic and/or some of which can cause heritable mutations.
It is not known how this exposure might translate into increases in mutation rates (and to what degree this might contribute to the rates of genetic diseases). It would be interesting to estimate genome-wide mutation rates, in humans and other species if possible, over the last few centuries by comparing relatives sharing DNA sequences that are connected by different numbers of generations before and after certain points in history to see if there is a measurable effect.