Vox posted an article, "The 7 biggest problems facing science, according to 270 scientists". I would have cast some of it differently and there are some alternative issues I might have focused on but it is worth reading over. It closely mirrors a conversation I had with a grad student last week about struggling to deal with a feeling of cynicism and pessimism in science versus trying to stay positive and focused on research. The section headings are copied below to give you a feeling of what is discussed.
Category Archives: Uncategorized
Can bacteria or parasites take advantage of RNAi against host genomes?
This is an idea I've had floating around in the back of my mind for a few years now. I keep some ideas secret in the short-run because I hope to be able to investigate them some day. However, I also have to face reality, with my teaching load and limited research funding there are a wide range of projects that I simply won't be able to follow up on. I figured it would be better to just put the idea out there so someone can check into this if they want.
RNA interference is a widely used and very useful genetics tool where gene expression can be reduced by double stranded RNA that matches the mRNA of the target gene. There is a great deal of literature on this and I am not going to attempt a summary or review of this technology and its natural role here. Instead I want to focus on a curious fact. For a wide range of species you can simply feed bacteria to the organism that have been modified to express double-stranded RNA and this can create phenotypes by silencing certain genes.
Okay, if this is so easy and straightforward (and quite short sequences of RNA can accomplish this) have any bacteria evolved to take advantage of inactivating genes of a host Eukaryote? Perhaps as a pathogen to block immunity and promote infection, or in a more symbiotic role to tweak host phenotypes? For that matter have any Eukaryotic parasites evolved this ability to excrete dsRNA or antisense RNA to alter host phenotypes? Part of this is a comparative genomics question and if candidate sites are found the follow-up study of activating or inactivating the gene sequence can be done to see if there is a response across species.
Culex Egg Rafts
Culex mosquitoes eggs stick together and are laid in "rafts" that float on the surface of water. In the picture above are four freshly laid egg rafts from our lab mosquito colony, each laid by a single female. They are on the end of a paintbrush that we used to lift them out of the water. They get darker as they age. The two lower rafts are almost the same age; the dark one above them is older and the very light one at the top is less than 1/2 an hour old. To prepare them for microinjection you want to use the very youngest one like the raft at the top. They are seperated from each other and arranged on a glass slide and injected using a microscope and micromanipulator for fine detailed control. They also harden as they age and the light ones can be injected without breaking the thin glass needle that is used. Once they harden you have to use a brief treatment with bleach to remove the out egg surface (chorion) which lowers the rate of survival.
The Square Root of Two
The root of your first period you Must place in quote, if you work true; Whose square from your said period then You must subtract; and to the remain Another period being brought, You must divide as here is taught, By the double of your quote, but see Your unit's place you do leave free; Which place will be supplied by the Square Of your next quoted figure there: Next multiply, subtract, and then Repeat your work unto the end; And if your number be irrational, Add pairs of cyphers for a decimal. - John Hill, 1772, Arithmetick, both in the theory and practice: made plain and easy in all the common and useful rules
This post has nothing to do with genetics or biology, just math. However, I enjoy thinking about math topics from time to time. This is a classic, an example of an irrational number, that goes back to the ancient Greeks. Just to lay it out, the square root of two is an irrational number that is made up of an infinite sequence of non-repeating digits:  . We can prove that it is an irrational number, which have odd properties, and this post is a way to try to better understand this.
. We can prove that it is an irrational number, which have odd properties, and this post is a way to try to better understand this.
The poem above is one method to estimate the square root of a number but an even older algorithm is known as the "Babylonian method." It is very simple and can quickly give reasonably accurate results. 1) Start with a guess of what the square root might be. 2) Divide the original number you are finding the square root of by this guess. 3) Average the resulting number and your guess. 4) Use the average as your new guess and repeat. 5) Stop when you have enough decimal places for the estimate.
To illustrate I will "guess" that the square root of two is one.






In just a couple of steps we have a very accurate estimate of the square root. This was done by the Babylonians 3,700 years ago (link and link). Now let's shift gears and think about tile geometry.
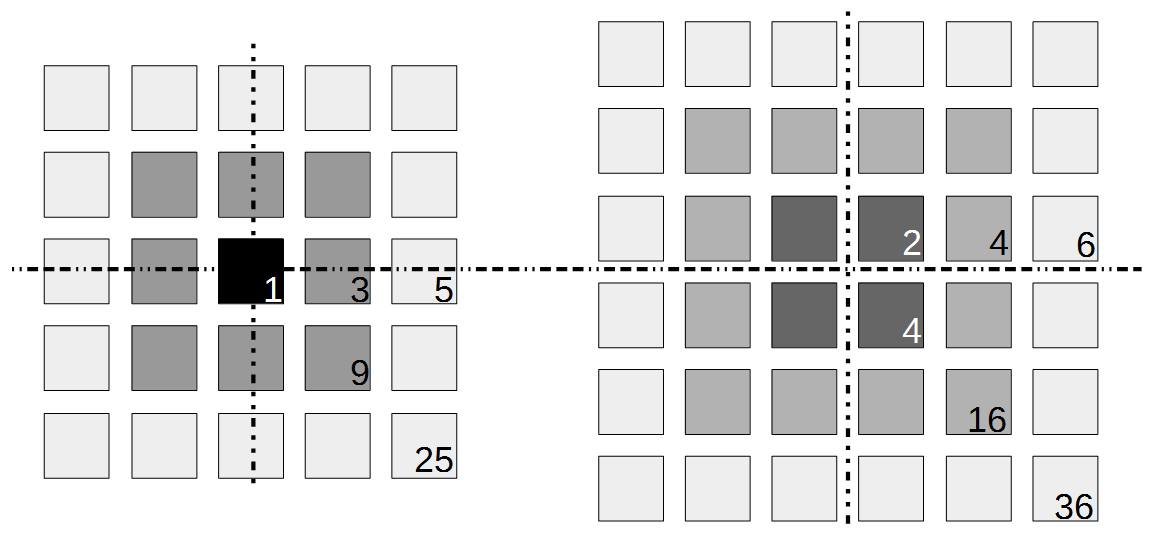
There are two ways to make larger squares out of tiles. You can start with a single tile and add squares around it. Or you can start with zero tiles and add squares around it. Notice that the width of the first kind of square is always an odd number, 1, 3, 5, ... and the width of the second kind of square is always an even number, 0, 2, 4, 6, ... . The square of these numbers are also always odd (1, 9, 25, ...) or even (0, 4, 16, 36, ...). So squaring an odd number always results in an odd number and squaring an even number always results in an even number. You can see this in a kind of visual proof. Evenly folding an odd square together breaks a line of tiles in the middle. However, folding an even square can be done evenly without breaking any tiles. (By the way, the figure contains an optical illusion---the Hermann grid illusion. There are "ghost" dots between the corners of the squares that disappear when you look directly at them.)
Now that we know this rule about the evenness and oddness of tiles in a square we can solve for the square root of two.
Represent the square root of two as a ratio of integers.

Square both sides.

Rearrange.

Realize that since the square of 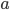 is even (the equation tells us that 2 is a factor of
is even (the equation tells us that 2 is a factor of 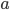 )
) 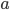 must also be even and can be factored into two and some other number
must also be even and can be factored into two and some other number  .
.

Substitute in the new definition of 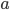 .
.

Solve.

Rearrange.

Simplify.

Realize that since the square of  is even
is even  must also be even and two along with another number
must also be even and two along with another number 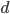 are factors of
are factors of  .
.

Substitute back in.

Cancel out two.

Using the same logic we can show that both  and
and 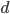 are even numbers, with two as a factor, and this reduction by halves will go on forever.
are even numbers, with two as a factor, and this reduction by halves will go on forever.
A lot of numbers we are used to can be represented by a ratio of integers, e.g.  . And an integer can be factored into a finite set of prime numbers, e.g.
. And an integer can be factored into a finite set of prime numbers, e.g.  . However, the ratio that represents
. However, the ratio that represents  is not the type of number we are used to. Both the numerator and denominator are infinitely large. We can extract an infinite number of factors out of each, 2 being the example here.
is not the type of number we are used to. Both the numerator and denominator are infinitely large. We can extract an infinite number of factors out of each, 2 being the example here.
Another example of an irrational (non-repeated in decimal form) number is  .
. 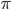 can be approximated by ratios of integers.
can be approximated by ratios of integers.



As the integers in the ratio become larger the approximations become more accurate, they are able to make finer and finer over- or under-corrections to the target, but they will always eventually end up in a repeating sequence because they are integers. To be exactly equal with complete accuracy the ratios that represent an irrational number have to be infinitely large. And we proved above that the numbers that make up the ratio representing the square root of two contain an infinite number of twos multiplied together (among other numbers) and so are infinitely large.
The existence of irrational numbers, that cannot be represented as a ratio of integers, is supposed to have vexed the ancient Greeks with the story of Hippasus. He was supposed to have been killed for his discovery of these strange numbers. And, they get stranger still.
Georg Cantor realized that, while the rational numbers were, essentially by definition, infinite in number, for each rational number there was an infinite number of irrational numbers. So, the number of irrational numbers is infinitely larger than the number of rational numbers, even though both are infinite in number (the number of rational numbers is a countable infinity while the irrational numbers are uncountable).
It may seem strange that there are multiple infinities that are not equal to each other---if it's infinite it's infinite right. Think of the positive integers, 1, 2, 3, 4, etc. there are an infinite number of these. However, for each of these, 3 for example, we could make a set of ratios, 3/1, 3/2, 3/3, 3/4, etc. and there would be an infinite number for each of the infinite integers. The number of integer ratios is infinitely larger than the number of infinite integers, even though there are an infinite number of integers. (However, both of these follow a logical sequence and could in theory be counted if we had infinite time and patience) Now imagine that we wrote out all of the integer ratios, the rational numbers, in decimal form. They will form a repeating structure.
22/7 = 3. 142857 142857 142857 142857 142857 142857 ...
There are an infinite number of positions where the decimal can be changed to break the repeating unit, making it irrational, and this can be done in an infinite number of ways
22/7 ≠ 3. 142887 142857 142157 142857 142857 742857 ...
22/7 ≠ 3. 142857 142857 142857 142857 142857 142337 ...
22/7 ≠ 3. 142857 842857 141856 142857 142857 142856 ...
etc...
There is not necessarily a logical order to go through all possibilities, there are simply too many ways to break up the infinitely long repeating structure, which introduces a new kind of uncountable infinity, even if we had infinite time and patience. So, for each rational number, a ratio of integers, there is an uncountable infinite number of irrational numbers.
Since the number of irrational numbers is so much larger than the rational ones, if we threw a dart at all the the rational and irrational numbers combined we are more likely, with essential certainty, to hit an irrational number at random. Therefore, we shouldn't be surprised that irrational numbers come up so often in mathematics. If it is not tied down to a direct construction from integers (e.g. the sides of a square with the first side set equal to one versus the circumference of a circle, natural logs, golden ratios, square roots of (non-perfect-square) integers) then it almost has to be irrational. In fact isn't it, in a sense, stranger that some things work out so simply like lengths of 3, 4, and 5 can form the sides of a right triangle (another perfect square exception, where two perfect squares (9 and 16) add up to a third perfect square (25), these are Pythagorean triples which are generalized in Fermat's last theorem---that this cannot be done with cubes, etc., and only works for some squares). This suggests that the square roots of numbers are on the edge of being constrained between a direct construction from integers (perfect squares and Pythagorean triples) and the freedom to be any type of number (the square root of all other integers and the irrational side of some right triangles, like 1, 1, and  ). This may be related to being defined in a simpler (and more constrained) two-dimensional geometry since there are no integers that can add up in this way in three or more dimensions (see Fermat's Last Theorem).
). This may be related to being defined in a simpler (and more constrained) two-dimensional geometry since there are no integers that can add up in this way in three or more dimensions (see Fermat's Last Theorem).
There might be a parallel, in a sense, with heterclinic cycles in two-dimensional state space. These are deterministic and seem to be well ordered (they are often asymptotically stable) but the trajectory never moves through the same point twice. It is something that is on the edge of, but not quite, a chaotic system (on the edge of being constrained and the freedom of unpredictably arriving at any value possible); and, for continuous dynamical systems at least three dimensions are required for chaotic behaviors. But I will save that for another post.
DNA Day 2016 and the Structure of DNA
April 25 is an informal "DNA Day" holiday---the date in 1953 when Watson et al., Franklin and Gosling, and Wilkins et al. were published describing the structure of DNA. The Genomics Sections or the Hawai'i Department of Health hosted an event on campus and I, among others, gave a short presentation. I was asked to go over a couple of classes related to genetics in the UH Manoa Department of Biology and to mention a couple of research projects in the lab. A copy of my slides are uploaded here.
I purposely delayed making the slides available as they contained some unpublished data. I am trying to make all of my presentations freely available, but there is some tension in doing this right away when they contain unpublished data. However, Aki Laruson just presented his results at the recent Evolution conference in Austin, Texas; Michael Wallstrom has a paper under revision; and, Gert de Couet and I have a manuscript rapidly getting closer to submission so it felt right to post the slides at this point.
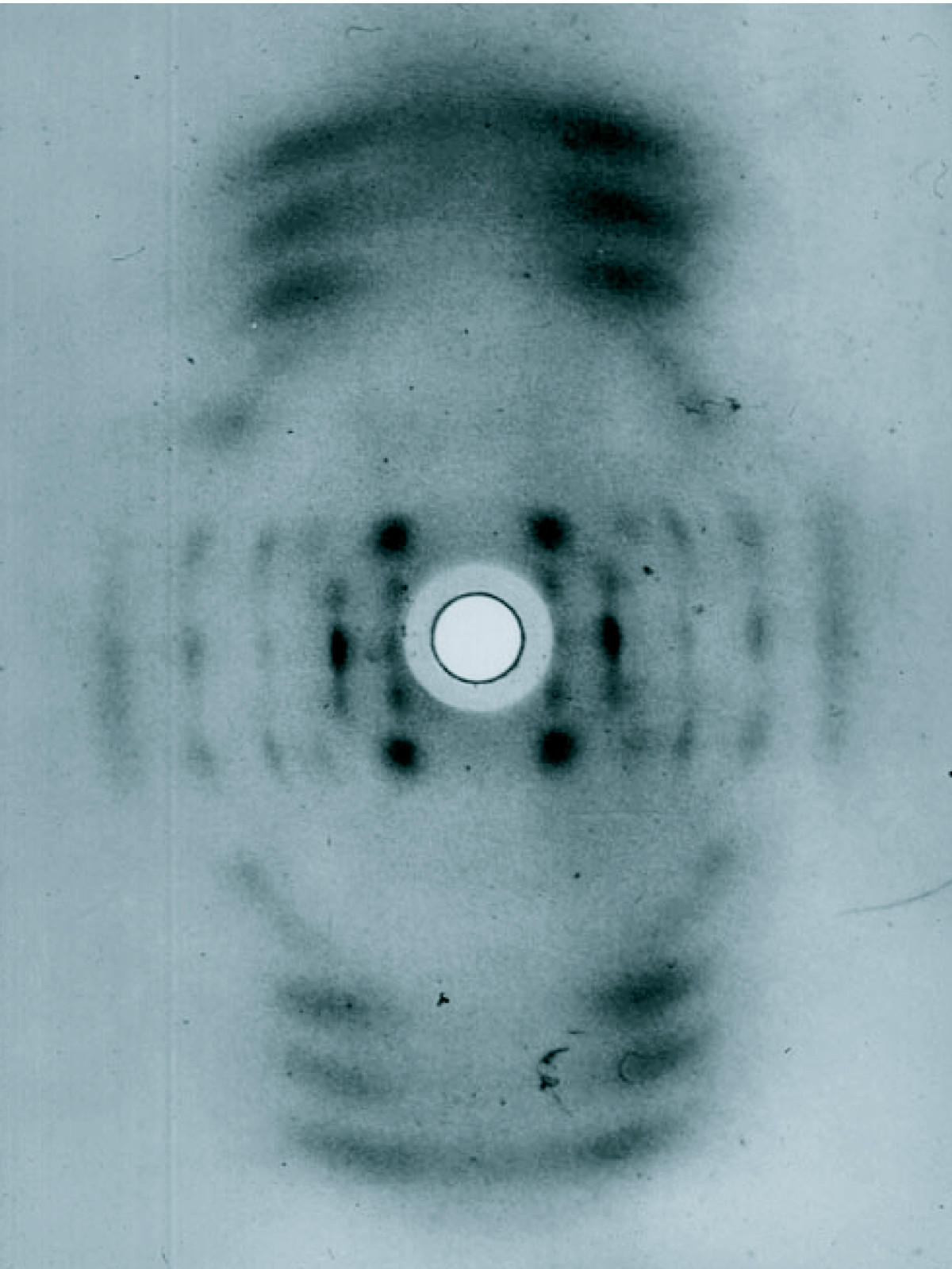
Speaking of the structure of DNA. I like to ask my students in class who made this image below, the first X-ray crystallography of the structure of DNA?
Was it:
A) James Watson
B) Francis Crick
C) Rosalind Franklin
D) Raymond Gosling
E) Maurice Wilkins
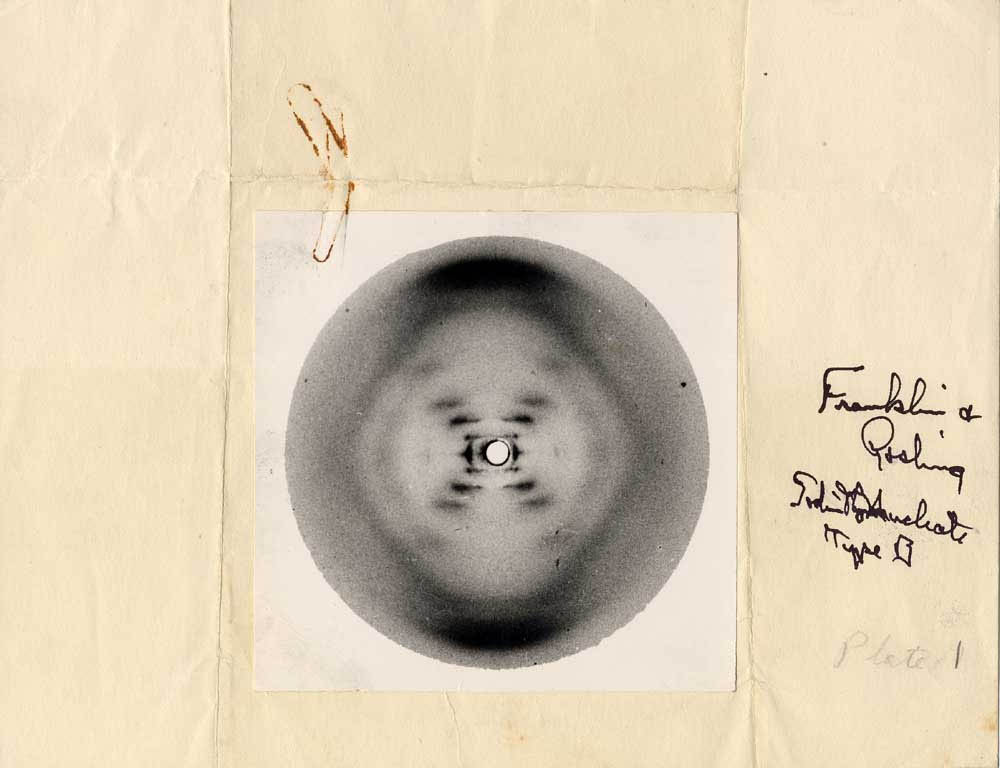
This is a fun question because so many people get it wrong. The story that Rosalind Franklin produced the image that Maurice Wilkins shared with Watson and Crick, and helped them determine the structure of DNA is well known. Most people select C) Rosalind Franklin. And, most people are aware that Watson, Crick, and Wilkins shared the 1962 Nobel Prize for Physiology or Medicine. However, practically no one is aware that Raymond Gosling is the one that actually first made images of DNA structures when he was a graduate student working in John Randall's lab. Later he was reassigned to work with Franklin and they produced the actual image (photograph 51) produced in 1952 that was shared with Watson. Notice the names written on the right side of the paper enclosing the film.
Some accounts give credit for this image to Franklin and some to Gosling. Since Gosling was the one to develop how to crystallize and image DNA, before Franklin arrived, and Gosling was a graduate student working for Franklin, I am fairly certain (unless new contrary evidence comes along) that this was actually made by Gosling.
Further Reading
Wilkins, M. H. F., Stokes, A. R., & Wilson, H. R. (1953). Molecular structure of deoxypentose nucleic acids. Nature, 171(4356), 738-740.
Loki's Castle and the New Tree of Life: Two Domains and the CPR Hidden Folk
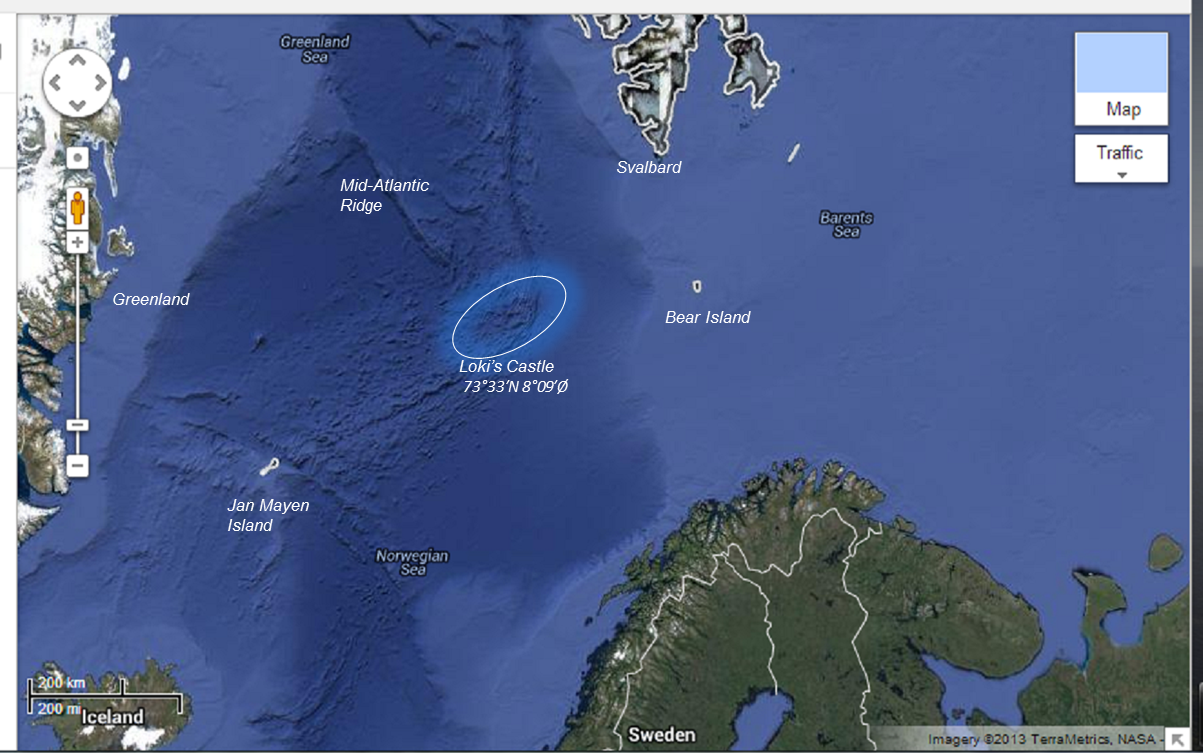
We all know who Loki is (the image above is from the 1700's Icelandic Manuscript, SÁM 66). Today he is seen as a trickster in Norse mythology. Loki had several children and was something like a great-uncle to another god Freyr in the mythological genealogy. Freyr was an ancestor of the Ynglings which was a dynasty of humans. The Ynglings transitioned from mythology to historical figures in the Middle Ages (incidentally one Yngling was Harald Fairhair who violently unified Norway and led to the exodus of families to Iceland, one descendant of which made the image of Loki above) so in a sense Loki's descendants are distant cousins of humans. ...and it turns out that Loki has a castle that was discovered in 2008.
 Loki's Castle is an undersea structure midway between Norway, Greenland, Jan Mayen, and Svalbard.
Loki's Castle is an undersea structure midway between Norway, Greenland, Jan Mayen, and Svalbard.
In 2015 Spang et al. recovered several unusual Archea from the sea floor near Loki's Castle and named them Lokiarchaeota. They share several genetic features with us, the Eukaryotes.
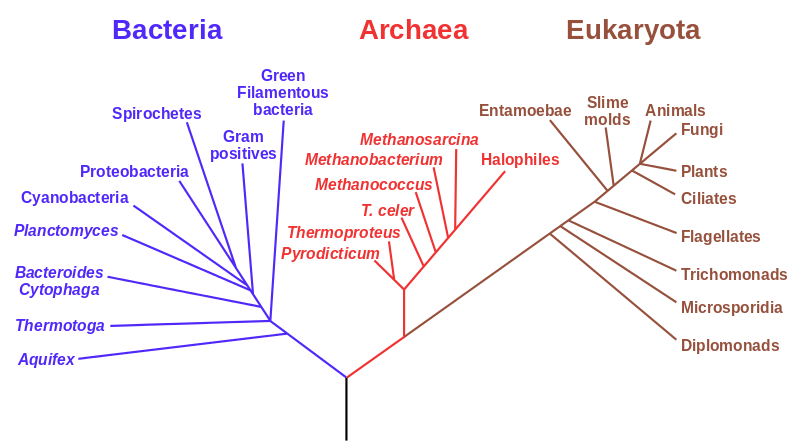
Many of us are now familiar with three domains within the tree of life in the figure above (it is tempting to make another mythological reference here---Tree-of-life---but I have probably already gone to far with the references to Loki and Freyr above): Bacteria, Archaea, and Eukaryota. We are most familiar with multicellular eukaryotes which make up the large forms of life we see around us, animals, plants, fungi. We know about the bacteria which are also common, around us, responsible for some human diseases, and required for healthy ecosystems and digestive tracts. The Archaea are more mysterious. They are single celled microbes that are around but not as abundant as bacteria; they are known for inhabiting extreme environments like high salt concentrations and high temperatures, but are also found in normal environments. In the phylogenetic reconstruction above the Archaea are closer related to Eukaryota than Bacteria but are still a distinct domain of life.
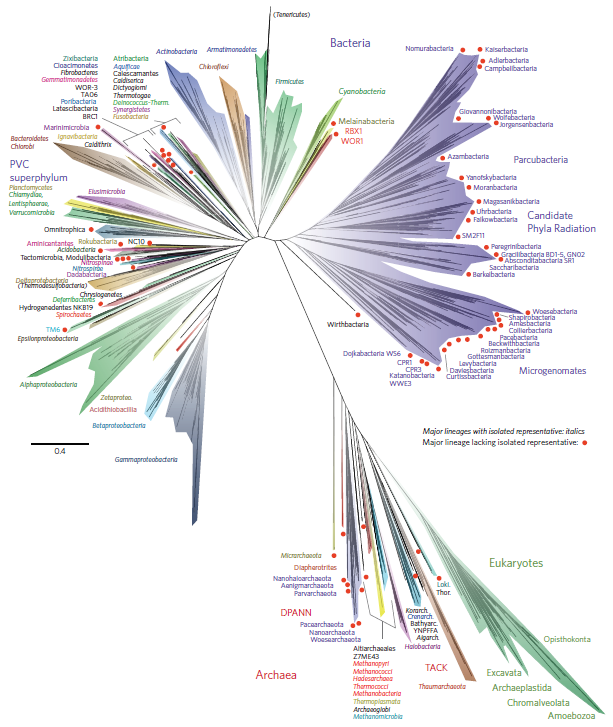
In recent years there have been hints here and there that this picture might be wrong and that the Archaea and Eukaryota are actually even more closely related. When the Lokiarchaeota from Loki's Castle were included in a different kind of phylogenetic tree there was a bit of a surprise.
The Lokiarchaeota are Archaea; however, genetically the "Lokis" are closer related to the Eukaryotes than to other Archaea. In a giant coincidence of taxon naming and mythology (with the right stretch here and there) we are in fact not too distant (within the scale of the tree of life) cousins of the Lokis! And, importantly, this places Eukaryotes within the Archaea; the Eukaryotes are not just related to the Archaea we are directly descended from the Archaea. Eukaryotes have complex cell structures with many types of membranes. The term "eu-karyon" means "true kernel" and refers to the cell nucleus where the chromosomes are stored surrounded by a membrane. There are also mitochondria that are surrounded by their own membranes (and have been secondarily lost in some Eukaryote protists like giardia)---and several other membrane bound organelles exist in Eukaryotic cells. The Lokiarchaeota's "genomes encode an expanded repertoire of eukaryotic signature proteins that are suggestive of sophisticated membrane remodelling capabilities" Spang et al. (2015).
Okay, so now the Eukaryotes are nested within the Arcaea and there are only two domains of life. Are there any other big surprises left?
Well... There have been hints in recent years that a strange group of bacteria exists. Sticking with the theme of this post the idea of a "hidden people" is common around the world's cultures (from Huldufólk Elves in Iceland to Jinn in the Middle East to the Cherokee Nvne'hi and the Menehune here in Hawai'i). These hidden people usually have unusual properties. There seems to be a large part of the tree of life that is widespread and exists, and likely has a large indirect effect on the world around us, but until recently has been completely invisible. And, it turns out that these appear to be very unusual cells.
Traditionally in order for new bacteria species to be formally described they need to first be cultured in the lab. However, it is well known that most bacteria that exist in the wild cannot be cultured with standard methods. Capturing DNA from the environment and sequencing it has revealed some strange sequences that appear to belong to bacteria but are very different from any described bacterial phyla---but, many of these mysterious bacteria, while diverse, appear to be closer related to each other than to the known bacteria and this has been referred to as the "Candidate Phyla Radiation" or CPR. Earlier this year Hug et al. attacked this problem head on and made an updated tree of life that includes a large number of these little known and uncultivated mysterious bacteria. A large and diverse sister group to all other bacteria is identified and corresponds to the CPR, adding a deep and diverse branch to the emerging picture of the tree of life.
Hug et al.'s tree confirmed the placement of Eukaryotes within Archaea (lower right) and added a tremendous amount of diversity to the Bacteria with the inclusion of the new CPR (upper right).
What are the CPR bacteria? They are indeed very strange. Brown et al. 2015 studied this in detail. The CPR tend to have greatly reduced genomes and cannot carry out some basic biochemical processes of a free living cell such as the synthesis of nucleotides and amino acids. They also have unusual ribosomal RNA sequences (containing introns and protein coding sequences) that would not have been detected using standard techniques. And, they contain signals that are indicative of parasitic cells that are not capable of living on their own. Taken together this helps to explain why it has not been possible to culture these bacteria independently of other cells. They probably depend upon close association with other cells for many basic molecules of life. An outstanding question is what is their role and importance in natural systems.
As a final note, this is likely not the end of the story. The world of viruses has been left out of this post completely and there are indications of undiscovered groups of highly divergent viruses out there in the environment (e.g. Wu et al. 2011).
Further reading
Brown, C. T., Hug, L. A., Thomas, B. C., Sharon, I., Castelle, C. J., Singh, A., … Banfield, J. F. (2015). Unusual biology across a group comprising more than 15% of domain Bacteria. Nature, 523(7559), 208–211. doi:10.1038/nature14486
Hug, L. A., Baker, B. J., Anantharaman, K., Brown, C. T., Probst, A. J., Castelle, C. J., … Banfield, J. F. (2016). A new view of the tree and life’s diversity, (April), Manuscript submitted for publication. doi:10.1038/nmicrobiol.2016.48
Nelson, W. C., & Stegen, J. C. (2015). The reduced genomes of Parcubacteria (OD1) contain signatures of a symbiotic lifestyle. Frontiers in Microbiology, 6(July), 713. doi:10.3389/fmicb.2015.00713
Spang, A., Saw, J. H., Jørgensen, S. L., Zaremba-Niedzwiedzka, K., Martijn, J., Lind, A. E., … Ettema, T. J. G. (2015). Complex archaea that bridge the gap between prokaryotes and eukaryotes. Nature, 521(7551), 173–179. doi:10.1038/nature14447
Williams, T. a, Foster, P. G., Cox, C. J., & Embley, T. M. (2013). An archaeal origin of eukaryotes supports only two primary domains of life. Nature, 504(7479), 231–6. doi:10.1038/nature12779
Wu, D., Wu, M., Halpern, A., Rusch, D. B., Yooseph, S., Frazier, M., … Eisen, J. A. (2011). Stalking the Fourth Domain in Metagenomic Data : Searching for , Discovering , and Interpreting Novel , Deep Branches in Marker Gene Phylogenetic Trees, 6(3). doi:10.1371/journal.pone.0018011
Undergraduate Showcase
I am still catching up on old posts from earlier in the semester.
On May 6th Michael Wallstrom and Zhaotong Xu presented their research at the "Undergraduate Showcase". This is held at the end of each semester at UH Manoa for undergrads to present research they have conducted.
Zhao worked on the cellular/developmental effects of PRAF2 ectopic expression in Drosophila and Michael worked on the phylogenetics and morphological description of a new Porifera species.
Richard G. Harrison
I (Floyd Reed) just learned that Rick Harrison passed away in April while on vacation in Australia. I came across a nice memorial article to him in the latest edition of Molecular Ecology. I did my first laboratory rotation in his lab when I first arrived in graduate school in the fall of 1996. After years of only reading and thinking about PCR I was able to set up my first PCR reaction in his lab in an RFLP project with gypsy moth (Lymantria dispar) samples from around the world (to try to identify the source of introduced populations). Later he became a member of my Ph.D. committee (for my Ecology and Evolution minor, the program I was in had Ph.D. minors). I still remember some of the other people in the lab; Steve Bogdanowicz (who first taught me a lot of molecular genetics lab skills), Chris Willett who is now at UNC Chapel Hill, Matt Hahn was an undergrad doing an experiment on copepods from lake sediments, and Mohamed Noor a postdoc in Chip Aquadro's lab collaborated with Rick on a cricket experiment. There were a few other people around the lab but I can't quite remember there names just now. One postdoc was working on generating a recombinant genetic map in beetles and later moved to Maryland, another grad student was working on a flying fish phylogeny... And of course there was the ram's skull with giant horns over the door to the darkroom where gels were visualized with UV.
Rick was a cheerful, intelligent man that was sometimes intimidating (to a new graduate student) but I did value and enjoy talking with him. He was very available, had a sense of humor (once he brought in some coprolites and asked the students to identify them), and seemed to have an endless supply of energy. He was interested in a wide range of subjects---I remember one conversation in particular about how broad versus how focused one should be on research subjects in the development of a career.
He is the second member of my graduate committee to pass away. Ken Kennedy (Physical Anthropology minor) passed away in 2014. It is hard to think that they are no longer with us.