I have been teaching myself R lately and had an idea for a simulation the other night so I've been working on this...

Many of us are familiar with the idea that eventually a room full of monkeys with typewriters will type the complete works of Shakespeare (the so-called infinite monkey theorem).  This has been used as an argument to illustrate ideas of biological evolution.  However, it falls far short.  The infinite monkey theorem works well for the intuition of random mutations, but it does not illustrate the power of selection and recombination to enrich the frequency of closer matches to a given text in a population (for mutation then to act upon).

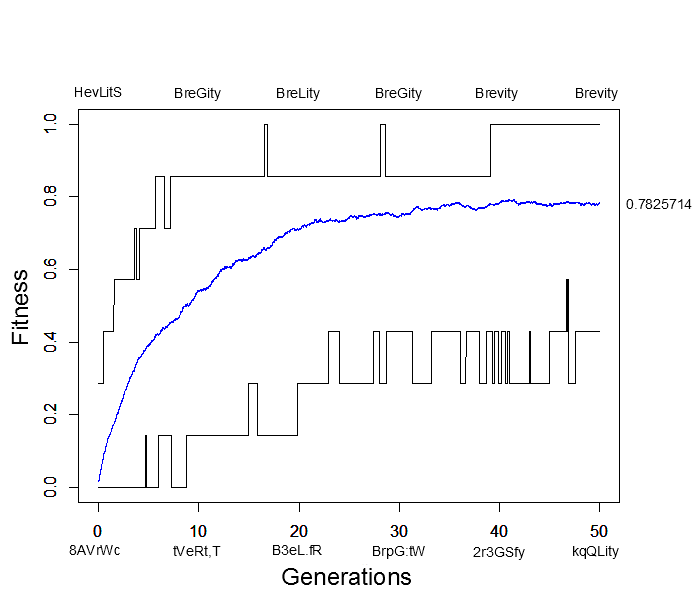
I wrote a script to try to illustrate this and evolved seven random letters to the word "Brevity."  This used random mutation, assigned relative fitness values to the sequences based on how many letters matched "Brevity," and recombined sequences randomly in the population.  Here is a plot of how the simulation preformed.  The average fitness in the population is shown by the blue line, the maximum fitness over all sequences is the upper line in the plot and the minimum fitness is the lower line.  Examples of the maximally and minimally fit sequences are given above and below the plot every ten generations.

This simulation was based on 500 sequences (or the equivalent of 250 diploid individuals) with a per generation, per character mutation rate of 2% and a per generation, per sequence recombination rate of 50%.  In less than 40 generations the population contained perfectly matching individuals spelling out "Brevity" from a starting best match of "HevLitS" in the first generation.  However, the population appears to have reached an apparent fitness equilibrium of close to 80% and poorly matching (40% fitness) sequences such as "kqQLity" remain at generation 50.  This is much sorter than the complete works of Shakespeare; however, it is also clear that the target "Brevity" was arrived at much faster with selection in a population than by just random mutation.

In fact, the target sequence was arrived at a couple of times, even briefly before 20 generations, but then disappeared again before the longer term arrival at 40 generations.  This illustrates one result of population genetics, that even though a new mutation may be more fit than any other versions (alleles) in the population, it is actually more likely to be lost by genetic drift (evolutionary sampling error) in the following generations than to increase dramatically in frequency.

What would happen if the simulation were allowed to run for much longer, say 500, 5,000 or even five million generations?  Would the average fitness eventually reach 100% with the entire population made up of the target "Brevity" (with the occasional rare mutation of course)?  An easier way to answer this than running the simulation for a very long time is to start the population with all perfect matches and see how closely it remains at this peak starting point.  Here is the result (under the same parameter values as the simulation result above):

Immediately the average fitness drops dramatically with sequences like "jrpvVty" appearing by generation 10.  At generation 50 the population arrives at a fitness near 85% of the maximum possible with lower bound fitnesses of 40%.  This is not far away from the near 80% arrived at before (also with a lower bound of 40%).  This illustrates the concept of "mutational load" in a population---that the average fitness will be quite a bit less than the theoretical maximum at mutation-selection equilibrium.  It takes time for deleterious mutations to be purged by selection and the net effect is a sizable reduction in fitness, in the case an average reduction of 15% to 20% from the maximum possible.

I am planning to continue discussing this in a few more posts.  This simulation might be a good way to illuminate the effects of population size,  mutation rates, recombination rates, and genome size on the evolutionary trajectory of a population.

While making this post I also inadvertently learned about a similar simulation called the "weasel program" by Richard Dawkins.  However, there are some important differences in the algorithm.  I also plan on discussing some ways the process of selection can be simulated---I came across some alternatives to the way natural evolution is typically modeled that dramatically change the trajectory of average population fitness, including the framework used by Dawkins.

Here is the R source code if you want to play around with it yourself:

# output the results to a text file if printout set to 1, 0 otherwise
# you should change the path to match your directory structure
# (it runs faster without the text output)
printout=1
if(printout){
  sink("C:\\Users\\Floyd\\Desktop\\backup\\work\\typewriter\\monkey_type_7_out.txt", 
    append=TRUE, split=TRUE)
}

length=7 # sequence length
n=500 # number of seequences
mut=50 # inverse mutation rate, one out of #
rec=2 # inverse recombination rate, one out of #
step=n*50 # "generations" in a Moran model

# store the population of sequences
pop=matrix(0,nrow=n,ncol=length)
# a vector of sequences
fit=matrix(0,nrow=n,ncol=1)

# set initial random sequences
for(i in 1:n){
  x<- sample(c(0:9, letters, LETTERS," ",".",",",":"),
             length, replace=TRUE)
  pop[i, ]=x
}

# keep track of fitnesses and generations during the run
runbestfit<-numeric() # best fitness
runavefit<-numeric() # average fitness
runleastfit<-numeric() # least fit
rungen<-numeric() # generations

target<-"Brevity" # target sequence

# divide into characters in a matrix for testing
targ<-strsplit(target, "")
t<-matrix(unlist(targ))

# if(1) sets population to all match target for testing
# if(0) turns this off
if(0){
  for(j in 1:n){
    for(i in 1:length){
      pop[j,i]=t[i]
    }
  }
}

# loop through time steps
for(s in 1:step){

  rungen[s]=s/n # generations defined as n time steps

  badfit=length
  badfitind=1
  maxfit=0
  maxfitind=1
  matchsum=0
  # loop through each position and add up if a match exists
  for(j in 1:n){
    match=0
    for(i in 1:length){
      if(t[i]==pop[j,i]){match=match+1}
    }
    matchsum=matchsum+match
    if(match>maxfit){
      maxfit=match
      maxfitind=j
    }
    if(match<badfit){
      badfit=match
      badfitind=j
    }
  }
  bestexample<-paste(pop[maxfitind,], collapse="")
  worstexample<-paste(pop[badfitind,], collapse="")
  runavefit[s]=matchsum/(n*length)

  # report current status
  if(printout){
    print(paste(s/n, "best ", bestexample))
    print(paste(s/n, "worst", worstexample))
  }

  #pick random individual to copy from weighted by relative fitness
  randfitpoint=sample(matchsum,1)
  repind=1
  matchsum=0
  for(j in 1:n){
    match=0
    for(i in 1:length){
      if(t[i]==pop[j,i]){match=match+1}
    }
    matchsum=matchsum+match
    if(matchsum>=randfitpoint){
      repind=j
      break
    }
  }

  # pick random individual to be replaced
  pick=sample(n,1)
  for(i in 1:length){
    pop[pick,i]=pop[repind,i] # best way to represent natural population (?)
  }

  # add mutations to the replicating sequence
  for(i in 1:length){
    m=sample(mut,1)
    if(m==1){
      x<- sample(c(0:9, letters, LETTERS," ",".",",",":"),
                   1, replace=TRUE)
      pop[pick,i]=x
    }
  }

  # add recombination with another sequence to the replicating sequence
    r=sample(rec,1)
    if(r==1){
      another=sample(n,1)
      location=sample(length,1)
      for(i in location:length){
        temp=pop[pick,i]
        pop[pick,i]=pop[another,i]
        pop[another,i]=temp
      }
    }

  # update best and least fit
  runbestfit[s]=maxfit/length
  runleastfit[s]=badfit/length

  # update plot of results
  # only every 50 time steps so it doesn't run too slowly
  if(s%%50==0){
    plot(rungen,runbestfit,type="l",xlab="generation",ylab="fitness",ylim=c(0,1))
    par(new=T)
    plot(rungen,runavefit,type="l",col='blue',xlab=" ",ylab=" ",ylim=c(0,1))
    par(new=T)
    plot(rungen,runleastfit,type="l",lwd=0.1,xlab=" ",ylab=" ",ylim=c(0,1))
  }

  # report current average fitness
  if(printout){print(runavefit[s])}
}