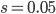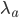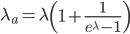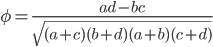This is derived from a class in am involved in this semester with Justin Walguarnery, ZOOL 490 "Origin and Future of Life." We started off by going over some attempts to define life. I wondered if a "living document" could participate in defining life. The original text is below.
Can a living thing help define life?
February 14, 2018
Abstract
What is life? The field of biology does not have a generally accepted definition of life. This document proposes a working definition of life and applies it to several examples and counter examples. Finally, a new experiment is proposed to attempt to harness a living system to help humans define life.
Introduction
The line separating living versus non-living is hard to define despite many attempts (e.g., Schrödinger 1944; Korzeniewski 2001; Ruiz-Mirazo et al. 2004; Macklem & Seely 2010). Definitions do not exist on their own; they are a tool used by humans. Definitions help shape human thought, and useful definitions help us to think about the essential relationships between things. Good definitions promote additional insights that may not have been apparent before. These definitions do not need to be mutually exclusive and should be used according to their utility towards a thought or idea. Defining a whale as a fish highlights its shape (fins, tail) and environment (marine, primarily underwater). A whale as a mammal highlights its evolutionary relationship with other placental mammals and traits such as air breathing, warm blooded, live birth, etc. However, we can transcend to another level and call a whale (and all mammals) a fish to illustrate their evolutionary relationship and realize that we ourselves are actually highly modified fish (Shubin 2008). Viewing a bird as a dinosaur (Chiappe 2009), or a tree as a carbon crystal which has grown out of an atmospheric solution of carbon dioxide, leads to some poetic, surprising, and sometimes insightful perspectives that suggest alternative lines of thought to explore.
Proposed definition:
1) Living things are capable of using resources from their environment to produce multiple copies of themselves with a level of complexity that allows for infinite possible heritable alterations.
2) These heritable alterations can result in unexpected emergent properties and can affect relative reproductive success among their copies.
3) The plans or instructions used to make a new organism are not separate from, but are linked to and share, the reproductive fate of the new organism.
Examples of life
Cells—cells are considered the basic unit of life on Earth and there is no argument among biologists that cells are examples of living things. Cells capture energy and materials from their environment and reproduce. Biology is full of the presumably ultimately infinite complexity of species that cells can give rise to. The problem with cells are that they have become equated with life in some definitions—if it is not a cell it is not alive—and this has likely profoundly biased our concept of what life is and is not. The definition used here does not make a distinction between autotrophs, cells that can produce all they need from non-living material, and heterotrophs which depend on other cells for energy and materials. This lack of a distinction is very important both in this definition of life and for many of the examples to follow. Other cells are a part of many cells’ environments, which they make use of in order to reproduce. The definition of life used here recursively includes organisms that depend on other organisms.
Viruses—viruses also use their environment, namely certain types of cells depending on the virus, to make copies of themselves. Simply because a virus depends on another cell for reproduction does not mean that it is not living. The same could also be said for humans. We, along with the vast majority of life on Earth, ultimately depend on other cells to survive—and we certainly consider ourselves to be living. If humans are living, viruses are living. Viruses are also capable of extremely rapid evolution into a diversity of forms that affect their reproduction in an ever-changing immune response from cells (e.g., Gong et al. 2013).
Computational life—humans, which depend on other cells to survive, have built computers, which currently depend on humans to operate. These computers can run simulations in which organisms compete with each other within a simulated environment to reproduce. If these simulations are sufficiently complex, so that there are an infinite number of possible “mutations” that affect survival and reproduction, with emergent unexpected properties, then these organisms are living according to the definition here (e.g., Yaeger 1994). It is not relevant that they exist within electronic states of a computer’s memory or that the course of evolution can be exactly recreated by starting from a saved earlier state.
Self replicating machines—humans use tools, which are simple machines, to build other machines. The last century has seen an increasing level of automation within factories, some of which build the very machines used in the robotic automation of factories. It would take a considerable amount of planning and design but it is entirely conceivable that a complex set of interacting machines could be built to collect their own energy in order to locate, mine, and refine raw materials. They could use these materials to produce components from a set of instructions, for building additional machines to collect energy, to locate more raw materials, and to repair and maintain existing tools and parts. It would be very complex, but in principle this could be accomplished. The idea has been proposed to build self-replicating factories on the moon, without humans present, in order to generate materials for space exploration (Chirikjian et al. 2002). If heritable “mutations” in the instructions used to make parts were possible, and it is hard to imagine how this could be completely prevented, then this system could be capable of limitless evolution and optimization as multiple factories began competing for resources. It is also easy to imagine specializations as some factories evolve to “steal” parts from other factories, etc. This type of system would be alive in every sense. The fact that it was initially designed by humans is not relevant to the definition used here. In fact, the initial factories would be autotrophs and even more alive than humans according to definitions of life that object to a reliance upon other cells. Similar to self-replicating moon factories, self-replicating spacecraft have been proposed (Tipler 1981). The machines would build copies of themselves from resources, such as comets, asteroids, and solar power, in space. This would also be technically challenging but there is no theoretical reason why this could not ultimately be accomplished. By constantly renewing and multiplying themselves, a greater region of space can be explored. All that is necessary to become living is for heritable changes to the designs, that affects the function of the probe, to be inherited with the machine so that the evolutionary trajectory is open ended and unpredictable—and incidentally potentially dangerous to us humans.
Social insects—insect colonies with a sterile “caste” of individuals are another challenging example. These workers are produced by a queen and only queens and drones can reproduce. The queen is dependent on the workers for long-term survival and reproduction. We humans, ironically, are comfortable with the idea of a multi-cellular organism, but have difficulty embracing the idea of a multi-bodied organism. (Bacterial scientists have a similar problem in thinking of the collection of all of the cells in our body as a single living unit⸮) Worker ants or bees are just extensions of the soma, the cells of an organism that are not in the germ-line which are passed on to the next generation. The entire colony is the unit of life. Extending this idea another step; some species of ants have domesticated, in every sense of the word, other species such as fungi and are now mutually reliant. Fungal farming is coupled with specific species and is copied from colony to new colony (e.g., Mueller et al. 1998). Here perhaps the unit of life is even larger and multi-species?
Transposable elements—these are a class of DNA sequences that reproduce themselves within a host’s genome. Much like a virus, they cannot function outside of a cell, yet they use their environment to reproduce and they evolve in potentially complex ways (e.g., Feschotte et al. 2003; Chuong et al. 2017).
Counter examples of life
Fire—in a sense fires can reproduce and multiply. However, there is no heritable functional complexity that can optimize reproduction. Therefore fire is not a living system.
Crystals—crystals grow and, if broken and distributed, perhaps by mechanical action such as waves, they can seed new crystal growth. However, like fire there is not an open-ended heritable complexity.
Prions—prions are proteins folded into a three dimensional configuration that induce similar proteins to also fold into the new configuration. In mammals prions are most often associated with disease; however, in fungi prions are used as a type of molecular memory to record past states and environmental conditions (Shorter & Lindquist 2005). Prions use their environment to make copies of themselves, but they do not pass on malleable heritable information that is capable of complex forms.
Robots—currently no robotic systems are alive. They are capable of complex behaviors and interactions. Robots can also be used to build other robots. However, if the plans used to build robots are static (e.g., the same physical copy is used), and not also copied along with the daughter robots and capable of change (and linked to the survival of the resulting copy), there is not a heritable system capable of unpredictable change, which is a requirement for this definition of life.
Evolved hardware—hardware exists that has been designed by an evolutionary process (e.g., Thompson 1996; Lohn 2005). How they work can be very hard to understand (by humans) and they can often outperform human-made designs. However, there is again not an open-ended heritable complexity passing from one design to the next.
RepRap—the RepRap project is an effort to make 3D printers out of parts largely made by 3D printers (Jones et al. 2011). This is a fun project and the printers are evolving to a certain extent, based on human-designed changes. However, the plans used to make the printers are not copied along with the printers, with mutation and alterations that are hertiable. The fate of the plans is not linked to the fate of the product. Thus, there is again a lack of heritable complexity that can lead to unpredictable unbounded evolution. Ultimately this could evolve into a living system but it is not there yet according to the definition used here.
Artificial Intelligence—the concept of highly developed AI is often confused with what might qualify as a living system. AI is or will soon be capable of intelligent communication, self awareness, and detailed knowledge about the world (Ferruchi et al. 2013; MacDonald 2015; Warwick & Shah 2016). However, what is missing is evolution and selection with heritable components. Often speculation about AI is confounded with assumptions of the need for self-preservation and even eventual hostility towards humans (e.g., Holley 2015); why? If AI was not shaped by evolution and competition for resources then there is no reason to suspect that it would have a motive of self-preservation. (How people might use AI is however another matter; Helbing 2017.) This is an anthropomorphic projection of human behaviors onto a nonliving system. If AI were designed to make copies of itself with heritable changes then it could become a living system, but perhaps we had better not do that.
Discussion
Often there is a confounding of complexity, intelligence, and replication with life. These are not the same. Life can be fairly simple (e.g., viruses and transposable elements, although one may hesitate to call these simple) if an appropriately complex environment, an operating system in the literal sense, is available. A key concept of this definition of life is being comfortable with various levels of dependence on other living things. There are layers of living things that depend upon each other, enabling additional forms of life. Just as the operating system of a computer allows computer viruses to flourish.
Living things are both able to replicate and have a sufficient degree of heritable complexity so that their evolutionary trajectory is unpredictable. Living objects are capable of evolving into an infinite number of states. Sufficient complexity is meant in the sense of Turing complete systems that are ultimately capable of simulating any computation (in an informational computation perspective, Turing 1937, sans the infinite memory requirement). Unpredictable is meant in the sense of chaotic systems, where approximate current states (with any degree of measurement uncertainty) cannot predict future states (cf., Werndl 2009). There is also a confounding of the question of the origin of cellular life on Earth, with a focus on nucleotides and early metabolic processes, with definitions of life. Here it is argued that the definition of life and the question of the origin of a specific form of life are distinctly different things.
Life does not exist on a scale from more living to less alive. This is a tempting elaboration to deal with viruses, heterotrophs, and social insects in alternative definitions of life. However, there is a discrete phase shift between systems that do not contain all the aspects of living systems (lacking in reproduction, heritable evolvability, complexity, etc.) and living systems that can use their environment to ultimately evolve endless possible forms. Some things might exist very close to this boundary—the edge between living and non-living. However, a key component is that the plans used to make multiple copies are themselves also copied and can change, and that their fate is linked to the fate of the copy.
Life is also consistent with design and extinction. Life under this definition is not limited to natural (non-human made) occurrences. Also, living things can ultimately go extinct—in fact the majority of cellular based species on Earth have gone extinct; yet, were they were no less living.
Many definitions of life discriminate between existence in physical reality versus … what‽ Can something in this universe ultimately exist outside of physical laws? Life, such as computer simulations, is not necessarily embedded within objective physical reality. But does this objective reality actually exist? Beginning with realizations that the Earth is not flat and the sun does not orbit the earth, even though it casually appears to us that this is so, we have uncovered more and more about the natural world that is not obvious to casual Earth-bound human observation, such as microorganisms, molecules, atoms, elementary particles, and the theoretical idea of quarks. Observations and ideas like particle entanglement in quantum mechanics, time-space trade-offs in relativity, energy-matter equivalence, challenge what we think of as objective reality and hint at deeper unfamiliar layers that underlie the world we see around us. Is it impossible to suppose that there are more fundamental physical worlds from which we would be viewed as, at best, a superficial simulation?
Some attempts at defining life utilize a thermodynamic perspective (e.g., Schrödinger 1944; Schneider & Kay 1994). However, nothing is free from physical laws, including thermodynamics, so we can entertain the idea that it is ultimately not useful to define life in thermodynamic terms to attempt to separate it from non-living systems. It is also a mistake to act as a reductionist of biology to the chemical and physical worlds. What is the more interesting perspective is a focus on the emergent properties of living systems in their own right, which is not simply deducible from physical and chemical laws (Dobzhansky 1964).
One final note, some of us humans are generally very focused on individualism, which again is ironic because we are multi-cellular and highly dependent upon each other and other species. This might profoundly bias our thinking about life and what constitutes living systems. We tend to think of physically discrete organisms as the unit of life (see the example of social insects above). However, we should work to try to relax that assumption. We should try to keep an open mind in order to recognize life around us and in the universe. This might take form in units that are physically distinct yet cooperate to reproduce and evolve (cf., Vaidya et al. 2012).
The experiment
There is another example of life that is perhaps unusual and surprising; yet, it fits the definition used here. Chain letters have existed for centuries, most recently in electronic form. They use their environment (humans) to make copies of themselves, i.e., reproduce. Usually this is in the form of exploiting human magical thinking in terms of good and/or bad luck related to copying and distribution of the text. This has been recognized and described by some in evolutionary and biological terms (Goodenough & Dawkins 1994; Bennett et al. 2003; VanArsdale 2016). It is also impossible to ignore similarities between chain letters and some religious texts and to speculate on the role of chain-letter-type dynamics both in text and in oral tradition in the evolution of religions (e.g., pp. 208, 221-222, 230-231, Budge 1904; pp. 96, 275, Goddard 1938; p. 172, Mizuno 1982; as pointed out by VanArsdale 2016; and possibly other examples, Psalms 96:3; Mark 16:15; Sahih al-Bukhari 6:61:510). Occasionally differences appear in chain letters that are copied to their offspring and influence their ability to reproduce (some of these differences are erroneous mistakes and some are purposefully made by humans). There is no obvious limit to the ways they can psychologically manipulate humans in order to reproduce (see the cookie recipe for a luck-free revenge-motivated example, Mikkelson 2016). This is not unlike some parasites that modify the behavior of their host organism to promote their own reproduction (Poulin 2010).
Can we utilize chain-letter-type dynamics for science? You can help make this document an example of life. Edit this manuscript with some changes and send it to some of your colleagues. This should be done without copyright by releasing it into the public domain (in current legal terms). Thereby, this document can use its environment (humans) to make copies of itself and reproduce. The most successful versions will be more likely to reproduce. What will be the result? Perhaps a refined definition of life can evolve from the evolution of this document (definitions are for human use and this document needs to utilize humans to reproduce), or it might likely take a trajectory towards attention seeking text unrelated to defining life. At the very least it is unpredictable and could be an interesting experiment in challenging ideas of what a living thing is and how we might recognize life, if it works at all. Please send a copy of the original version of the document you received and the modified copy you sent out to this address, life.defining.life@gmail.com , so that the evolution of this document can be monitored over time and the results made public.
References
Bennett, C. H., Li, M., & Ma, B. (2003). Chain letters & evolutionary histories. Scientific American, 288(6), 76-81.
Budge, E. A. W. (1904). The Gods of the Egyptians. Dover (1969), Vol. I & II.
Chiappe, Luis M. (2009). Downsized Dinosaurs: The Evolutionary Transition to Modern Birds. Evolution: Education and Outreach. 2(2): 248–256.
Chirikjian, G. S., Zhou, Y., & Suthakorn, J. (2002). Self-replicating robots for lunar development. IEEE/ASME Transactions on Mechatronics, 7(4), 462-472.
Chuong, E. B., Elde, N. C., & Feschotte, C. (2017). Regulatory activities of transposable elements: from conflicts to benefits. Nature Reviews Genetics, 18(2), 71.
Dobzhansky, T. (1964). Biology, Molecular and Organismic. American Zoologist 4, 443-452.
Ferrucci, D., Levas, A., Bagchi, S., Gondek, D., & Mueller, E. T. (2013). Watson: beyond Jeopardy!. Artificial Intelligence, 199, 93-105.
Feschotte, C., Swamy, L., & Wessler, S. R. (2003). Genome-wide analysis of mariner-like transposable elements in rice reveals complex relationships with stowaway miniature inverted repeat transposable elements (MITEs). Genetics, 163(2), 747-758.
Goddard, D. (1938). A Buddhist Bible. Boston: Beacon Press
Gong, L. I., Suchard, M. A., & Bloom, J. D. (2013). Stability-mediated epistasis constrains the evolution of an influenza protein. Elife, 2:e00631
Goodenough, O. R., & Dawkins, R. (1994). The 'St Jude' mind virus. Nature, 371(6492), 23.
Helbing, D., Frey, B. S., Gigerenzer, G., Hafen, E., Hagner, M., Hofstetter, Y., ... & Zwitter, A. (2017). Will democracy survive big data and artificial intelligence. Scientific American, 25.
Holley, P. (2015). Bill Gates on dangers of artificial intelligence:‘I don’t understand why some people are not concerned’. Washington Post, 29. https://www.washingtonpost.com/news/the-switch/wp/2015/01/28/bill-gates-on-dangers-of-artificial-intelligence-dont-understand-why-some-people-are-not-concerned/?utm_term=.7bff3b352aba
Jones, R., Haufe, P., Sells, E., Iravani, P., Olliver, V., Palmer, C., & Bowyer, A. (2011). RepRap–the replicating rapid prototyper. Robotica, 29(1), 177-191.
Korzeniewski, B. (2001). Cybernetic formulation of the definition of life. Journal of Theoretical Biology, 209(3), 275-286.
Lohn, J. D., Hornby, G. S., & Linden, D. S. (2005). An evolved antenna for deployment on NASA’s Space Technology 5 mission. In Genetic Programming Theory and Practice II. pp. 301-315. Springer US.
MacDonald, F. (2015). A robot has just passed a classic self-awareness test for the first time. Science Alert, 17. https://www.sciencealert.com/a-robot-has-just-passed-a-classic-self-awareness-test-for-the-first-time
Macklem, P. T., & Seely, A. (2010). Towards a definition of life. Perspectives in Biology and Medicine, 53(3), 330-340.
Mikkelson, B. (2016). Neiman Marcus $250 Cookie Recipe. https://www.snopes.com/business/consumer/cookie.asp
Mizuno, K. (1982). Buddhist Sutras: Origin, Development, Transmission. Tokyo: Kosei Publishing Co.
Mueller, U. G., Rehner, S. A., & Schultz, T. R. (1998). The evolution of agriculture in ants. Science, 281(5385), 2034-2038.
Poulin, R. (2010). Parasite manipulation of host behavior: an update and frequently asked questions. In Advances in the Study of Behavior (Vol. 41, pp. 151-186). Academic Press.
Ruiz-Mirazo, K., Peretó, J., & Moreno, A. (2004). A universal definition of life: autonomy and open-ended evolution. Origins of Life and Evolution of the Biosphere, 34(3), 323-346.
Schneider, E. D., & Kay, J. J. (1994). Life as a manifestation of the second law of thermodynamics. Mathematical and Computer Modeling, 19(6-8), 25-48.
Schrödinger, E. (1944). What Is Life? Cambridge University Press, Cambridge.
Shorter, J., & Lindquist, S. (2005). Prions as adaptive conduits of memory and inheritance. Nature Reviews Genetics, 6(6), 435.
Shubin, N. (2008). Your inner fish: a journey into the 3.5-billion-year history of the human body. Vintage.
Thompson, A. (1996, July). Silicon evolution. In Proceedings of the 1st Annual Conference on Genetic Programming (pp. 444-452). MIT press.
Tipler, F.J., 1981. Extraterrestrial Intelligent Beings do not Exist. Quarterly J. of the Royal Astronomical Society 21, 267-281.
Turing, A. M. (1937). On Computable Numbers, with an Application to the Entscheidungsproblem. Proceedings of the London Mathematical Society. 2. 42: 230–65.
Vaidya, N., Manapat, M. L., Chen, I. A., Xulvi-Brunet, R., Hayden, E. J., & Lehman, N. (2012). Spontaneous network formation among cooperative RNA replicators. Nature, 491(7422), 72.
VanArsdale, D. W. (2016) Chain Letter Evolution. http://www.silcom.com/~barnowl/chain-letter/evolution.html
Warwick, K., & Shah, H. (2016). Can machines think? A report on Turing test experiments at the Royal Society. Journal of Experimental & Theoretical Artificial Intelligence, 28(6), 989-1007.
Werndl, Charlotte (2009). What are the New Implications of Chaos for Unpredictability? The British Journal for the Philosophy of Science. 60 (1): 195–220.
Yaeger, L. (1994). Computational genetics, physiology, metabolism, neural systems, learning, vision, and behavior or Poly World: Life in a new context. In Santa Fe Institute Studies in the Sciences of Complexity-Proceedings Vol. 17, pp. 263-263. Addison-Wesley Publishing Co.