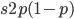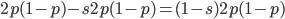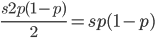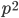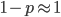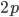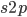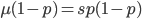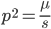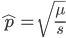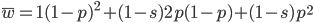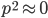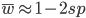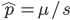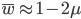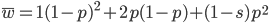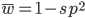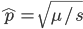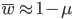I am jotting down some more recommendations for pursuing a tenure-track career in biology. I am a sample size of one, and there are other people that can do a much better job than myself in terms of career advice, but I have recently been successful in getting tenure and it doesn't hurt to share some thoughts, especially when they are fresh in my mind. Many things are obvious (publish as much as possible, get teaching experience, apply for funding, maximize a focus on "safer" projects that also have a higher impact in the field and can be done in less time, work in an area that you are naturally motivated in, etc.) so here I am naturally focusing on things that are perhaps less obvious or unnatural (at least to me). And, invariably some people will disagree with me, which is fine; I may be over-correcting on some aspect.
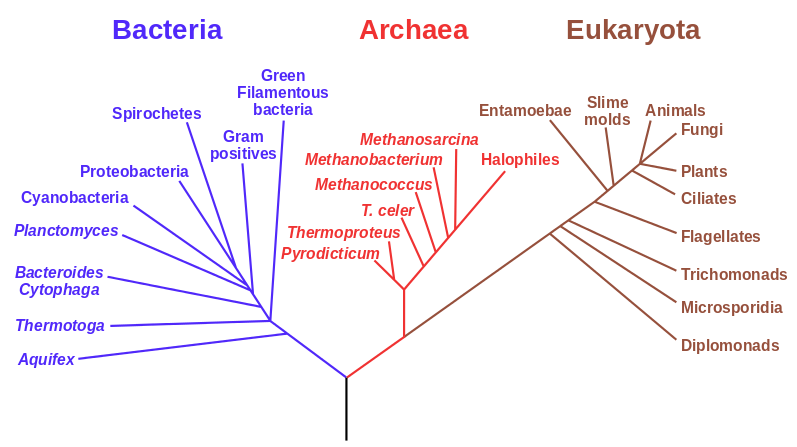
First of all here is a helpful graphic in terms of what to expect (the proportions of people in different positions and time spent in those positions) with a Ph.D. in biology in the US. For example, 10% of the people that start off in a Ph.D. program get a tenure-track position---and obviously less than that, perhaps as many as 8%, get tenure.

1) Networking
One of the things that is much clearer to me in recent years compared to when I started out is the importance of networking and advertising yourself. Something about this goes against my nature; I feel like your work should stand on its own merits or not and you shouldn't resort to tricks like using networks of individuals to get ahead, but it is very important to let people in a field know that you exist and that you are doing cool work. This does not mean only making connections with the established famous people in the field, although that doesn't hurt, but also getting to know a wide range of people in the same position as yourself. Some of these people eventually will be the established famous people in the field and they will be good connections to have. A very important part of this is attending meetings and always accepting invitations to visit other institutions. Remember that every talk is a job talk whether it seems like it or not. Advertising your work will stick in some peoples minds and down the road when they are on hiring/search committees it can affect the kind of research areas that they are looking for and you might even get invited to apply.
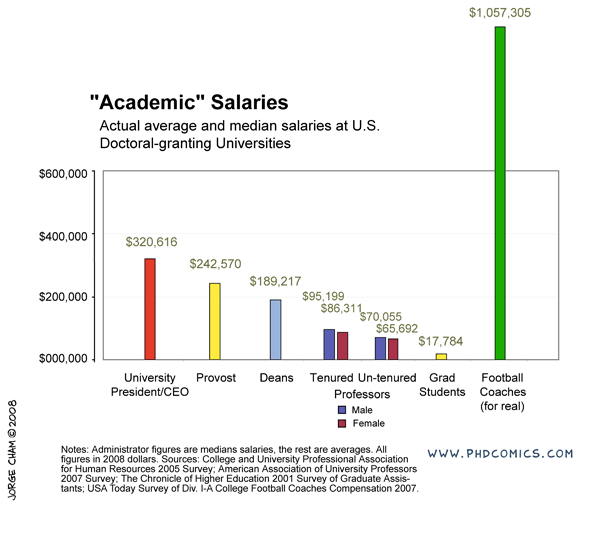
The challenge to this is financial (and take a good look at the levels of support for grad students in the comic above---this is true and not a joke---if your primary goal is a chance to make a lot of money then go into football). It is expensive to travel and to attend meetings. Sometimes you can pay for this off of a grant and sometimes you can get awards to help pay for this, but there is simply not enough support out there to go around and at some point you will have to pay for this yourself, which can be an added challenge if you also have dependents. As an example, I wanted to go to an international meeting in New Zealand. I applied for travel support but was turned down. The lab I was in agreed to cover the air fare (which I truly appreciated, it was a huge help and the majority of the expense) but I still needed more money to pay for a hotel, transportation in NZ, food, etc. I found a temporary night job and did that for a short while (keep in mind, many graduate students are not supposed to work outside jobs as a part of tuition waiver agreements but many secretly do anyway out of necessity) to save up enough for the trip. I attended the meeting and on the return I landed in LAX with exactly $5 left. That was it, no credit on credit cards or money in the bank were available; however, I was getting paid in the next day or two and I was getting picked up from the final airport on the east coast. I was thirsty and had a long layover, so I used it to buy a bottle of orange juice, drank that, and that was it, but I had made it to the meeting in NZ and back.
2) Establish yourself in a "narrow" field
Another factor that is much clearer to me now than it was years ago is the importance of staying within a defined area. Funding agencies, journal editors, and almost everyone in science say how important interdisciplinary work is---but don't fall for it too early in your career. It may in fact be important but unfortunately it is not what gets funding and gets published. This is another factor that goes against some part of my basic nature; I am curious about a wide range of subjects and enjoy thinking about very different projects. However, this has greatly slowed down my career advancement. I have changed fields from a Drosophila lab studying the effects of natural selection to human genetics studying gene-culture coevolution to designing gene-drive systems in insects AND natural history and evolution in the Indo-Pacific. A common theme throughout all of this is population genetics but this is too broad. Each time I switch to a new field I have to work to become "known" to people working in the field and this is an added challenge in getting grant funding and publications. It is well known that there is a very strong "Matthew Effect"[1] in science; there is a circular positive feedback where the people that are successful in a field become even more successful in a field simply because they are successful in the field (because funding is limited this has the counter negative feedback where people that are not well known cannot get established; also, a lot of success within a field is inherited from advisors). This has led to occasionally comical interactions where other scientists have "explained" published research to me that I actually carried out and published; they just forgot and/or didn't expect me to be the author of the article that they read. One of the coolest projects I have been involved in was literally drawn on a napkin over lunch; I drew out an experimental economics "game" that occurred to me. One of the other scientist at the table (who did this type of research) carried it out in his lab over the following months; we wrote it up and eventually it was published in PNAS; which was not bad. Later I had people ask me why I was an author on the manuscript despite---unknown to them---coming up with the idea, analyzing some of the results, and writing part of the manuscript, because they had pigeon-holed me and didn't expect that I could have anything to offer to an experimental economics project. I wish that science could be more truly interdisciplinary, but unfortunately, frankly, it will not help you to become established in your career. Rather, you should stay within what may seem like a painfully narrowly defined area and be incremental, changing just one or two aspects of your research at a time between projects (same question with a different method or same method with a different species/question, etc.). Either explore diverse areas very early, preferably as an undergrad or grad student, or wait until you are well established to broaden your active interests back out, do not do this as a postdoc or assistant professor---or if you are like me you will just ignore this advice anyway.
3) Honest advice on your CV
Find people that can give you feedback on your CV. Most importantly people that are not afraid to criticize you. Your CV is the most important record of your advancement in the field and you have to focus on developing it. Use someone else's as a template and copy its format. I obsessively updated mine every time I had a new publication or presentation. Also, don't be afraid to create new categories like "media impact" or "service to the field" and unashamedly brag on yourself; this is one of the places where it is appropriate and expected. (And, bragging on myself is another thing that I still working to overcome; I guess it is related to the culture I was raised in; however, modesty and humility are not rewarded in science.) I have relied on a few people over the years that were not advisors in any official sense and they have helped me tremendously, giving me pointers like I needed more publications or presentations and not to worry so much about grants, etc., at such and such a stage. Having mentoring advice, which is on you to seek out and establish a mentor relationship, is extremely important for people that are the first in their family to go into academia, without the family advice that some people benefit from.
4) Avoid moving between systems
This hurts me to say, but avoid moving internationally if possible. Unless you are a super-star where no matter what you do it will be seen as a plus (see Matthew effect[1]), moving between systems will only count against you. Here is my experience in this respect. After completing a Ph.D. in grad school I did a postdoc at the University of Maryland. I was working in human genetics with a focus on Africa. I had significant college loans that I was paying back and I applied for a competitive NIH loan repayment program for people working in health disparities research, with a catch that you have to remain working within academia for a certain period. All along I communicated with the NIH office that I was actively applying for my next academic position and would be changing institutions, and they told me that this was not a problem just to update the information with them once I moved (they never once told me that I could only move within the US; academia is very international; it is common to have a diverse range of nationalities working together within a lab).
I applied widely to many different job opportunities and finally landed a position as an "independent group leader" at a Max Planck Institute in Germany that was advertised as equivalent to an assistant professor position in the US (in this position I had my own lab, funding, independent research, applied for grants, taught classes, had students and postdocs, served on committees, etc.). In this new position I started a completely new line of research that was independent from my work in graduate school and independent from my postdoctoral work. I notified NIH of my new address and position and things immediately got weird. Suddenly there was a problem, since I was now employed in academia outside of the US (what choice did I have? this was the only job offer I had within academia, which is one of their requirements). Apparently, I was in violation of a rule that they had neglected to communicate to me, despite my communication with them that I was changing institutions in the near future. Apparently you are not allowed to work outside of the US or you can be fined. They threatened me with this fine, which was larger than the total amount I had in college loans in the first place. After some back and forth communicating they finally "forgave" me and I was kicked out of the repayment program after it had just started. Okay, so I had wasted a significant amount of time applying for this (when I could have been writing grant applications and manuscripts for publication) but compared to what they could have done to me I had dodged a bullet.
Jumping ahead, after working in Germany for a few years I applied for a new position and landed a tenure track job here at UH. However, my work in Germany was not counted as the equivalent of experience in an assistant professor position. I could not apply for tenure and promotion early based, partially, on this prior position. Some of the faculty in my new department referred to my work in Germany as a postdoc position (despite my corrections, I hired my own postdocs in Germany). They also insisted that many of my publications were "meaningless" for tenure because they were related to work that I had done in my previous lab in Germany (I guess they were thinking this work was done under a "postdoc advisor" ?). People construct scenarios that fit their expectations and it is difficult and tedious to try to change their minds. Also, my current graduate student in Germany could not move to my new lab because of visa/citizenship issues in her family. I was contacted by people wanting to work in my lab---in Germany---but they were not willing to move around the world and I was not known in Hawai'i and the West Coast. Essentially, my time in Germany establishing a new lab did not count and I had to start completely over.
But, I couldn't start over. I had received a federal grant from the DFG in Germany. Once you receive a federal grant as a PI you loose "young investigator" status with NSF (I talked with an NSF officer who confirmed this), which put me at a relative disadvantage to other new assistant professors...at the same time this DFG federal grant did not count towards tenure in my new position at UH. Also, I had been in labs, and helped write applications, that were funded by NIH. In Germany I learned how to apply to the DFG. Now I had to break into the NSF funding world with all of the unspoken rules, red flags, weird definitions, and key words that they were looking for (NSF "Broader Impacts" are very unusual compared to other funding agencies and are very strictly defined---e.g., I was criticized by reviewers for including broader impacts that were economic rather than strictly educational).
In an ideal world we could live and work internationally. I think this is something that should be encouraged, especially in science. However, in my experience it only counts against, and is turned against, you (people in power look for excuses to fit you into, or not fit you into, a particular category depending on their motivations, having an unusual background provides enough ambiguity to be flexible about this). Like the interdisciplinary advice above, either do this very early or wait until you are well established to make an international move.
5) Nepotism
I'm not sure that this is really advice but it is a non-obvious aspect of a career in science that is worth sharing. This is something that seems to be unique to academia (within the US). When you are hired to a faculty position there is a possibility of a "spousal hire." In other words finding a position for your spouse within the university. However, your spouse also has to be in academia with the credentials to be hired as a faculty member in a department. If your spouse works outside of academia or, as in my case, has had to delay their career advancement in order for you to advance (we could not afford to simultaneously attend graduate school, however, my wife has a psychology degree and experience working in academia both in research labs and as department support staff, but does not qualify to be hired at the tenure-track faculty level) this opportunity is not extended to you.
This is a very weird situation. I didn't even realize it was legal for institutions to openly embrace it when I started out in academia. It is brought on by how rare positions are within a specific research field, so that it is practically impossible for faculty-track couples that meet later in life (grad school or after) to be hired within their career in the same geographic location. However, it is obviously nepotism (not that there aren't some excellent people in science that are also spousal hires) and puts couples that have been married for longer and met earlier in their careers (and do not have family resources to help pay for an education) at a relative disadvantage.
6) Dealing with disabilities
We all have different challenges that we have to work to overcome. Here I can only speak from my own perspective but I intend this as a general statement. Like approximately 5% of the population I am dyslexic. I am very slow at reading and writing compared to most people, having to frequently reread sentences as I go; I also don't passively read text around me (like posted signs). This makes it a challenge to keep up with current literature and especially email (tricks like black or dark gray text on a yellow background help). I am also a horrible speller; I still have to look up the difference between discreet and discrete. I have had assess go wrong more than once in a manuscript and recently accidentally used salacious for siliceous (a different underline color should be used in text editors for words that are spelled correctly but can easily be the wrong word). This means that I simply have to dedicate more time in my schedule to reading and writing.
I am also partially deaf with a complete loss of hearing in one ear and some hearing loss in the other. One of the results of being monaural is that I cannot separate voices from background sounds, something that most people are able to do instinctively and cannot truly understand without experiencing it (plugging one ear is not the same, I do not have bone conduction of sounds which people with normal hearing still have and can use subconsciously to pick up on auditory cues). This is a social handicap but at the same time it is cryptic. I can hear people and understand them (I am also able to use lip reading to a certain extent) but in situations where there is significant background noise, especially when it is other human speech, it becomes very difficult to filter out what someone is saying---and repeatedly explaining this becomes both burdensome and prone to misinterpretation (imagine saying at a scientific meeting "I'm sorry but I can't understand what you're saying..." without time to explain). My wife and I have worked out some of our own hand signs to use in situations where I cannot hear, but this doesn't work for other people. Above I talked about how important it is to network and attend meetings; however, during the social parts of these meetings, where many people are talking together in a room, I cannot effectively communicate with other people, which can easily give the wrong impression. Also, during presentations when I am in the audience and there are questions from the audience I often cannot hear what people are asking because I cannot see their face while they are talking---this leads me to not saying anything because I am worried that I might repeat a question or comment that everyone else heard. Fortunately there are ways to address this. It is not easy but situations can be engineered where you can talk to people one-on-one or in a small group in a quiet area, "hey, let's get some lunch," or "coffee," etc. (Although, talking while eating leads to some people covering their mouth with their hand, which is a problem for lip readers.) Also, I have run into a surprising number of people just after a meeting at the airport, where they tend to be alone with unplanned time and it is a perfect opportunity to introduce yourself and have a conversation---I actively scan for these people now. I have run into a few (I can count on one hand) people that are also monaural in science. The specifics of this section are obviously not general advice, but the strategy, engineering or taking advantage of opportunities to overcome an issue, is what is intended.
1) 'In the sociology of science, "Matthew effect" was a term coined by Robert K. Merton to describe how, among other things, eminent scientists will often get more credit than a comparatively unknown researcher, even if their work is similar; it also means that credit will usually be given to researchers who are already famous. ... Merton furthermore argued that in the scientific community the Matthew effect reaches beyond simple reputation to influence the wider communication system, playing a part in social selection processes and resulting in a concentration of resources and talent.'
https://en.wikipedia.org/wiki/Matthew_effect#Sociology_of_science
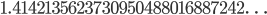 . We can prove that it is an irrational number, which have odd properties, and this post is a way to try to better understand this.
. We can prove that it is an irrational number, which have odd properties, and this post is a way to try to better understand this.
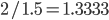
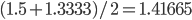
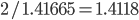

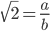
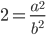
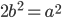
 is even (the equation tells us that 2 is a factor of
is even (the equation tells us that 2 is a factor of  )
)  must also be even and can be factored into two and some other number
must also be even and can be factored into two and some other number  .
.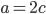
 .
.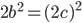
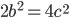
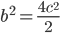
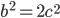
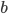 is even
is even 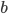 must also be even and two along with another number
must also be even and two along with another number 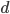 are factors of
are factors of 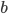 .
.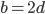
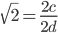
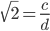
 and
and 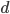 are even numbers, with two as a factor, and this reduction by halves will go on forever.
are even numbers, with two as a factor, and this reduction by halves will go on forever.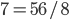 . And an integer can be factored into a finite set of prime numbers, e.g.
. And an integer can be factored into a finite set of prime numbers, e.g. 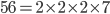 . However, the ratio that represents
. However, the ratio that represents 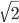 is not the type of number we are used to. Both the numerator and denominator are infinitely large. We can extract an infinite number of factors out of each, 2 being the example here.
is not the type of number we are used to. Both the numerator and denominator are infinitely large. We can extract an infinite number of factors out of each, 2 being the example here.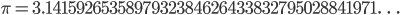 .
. 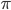 can be approximated by ratios of integers.
can be approximated by ratios of integers.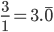

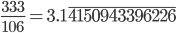
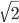 ). This may be related to being defined in a simpler (and more constrained) two-dimensional geometry since there are no integers that can add up in this way in three or more dimensions (see Fermat's Last Theorem).
). This may be related to being defined in a simpler (and more constrained) two-dimensional geometry since there are no integers that can add up in this way in three or more dimensions (see Fermat's Last Theorem).