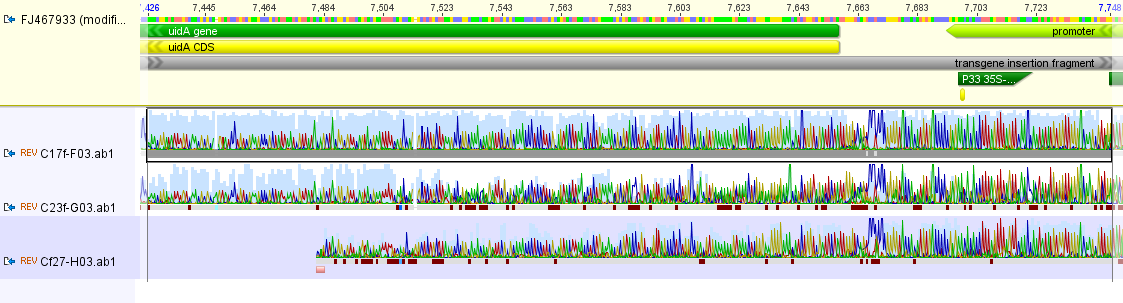
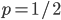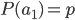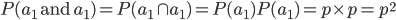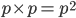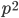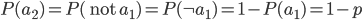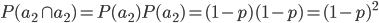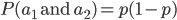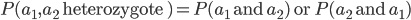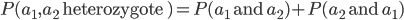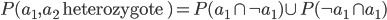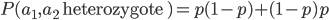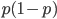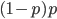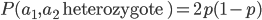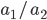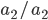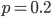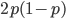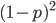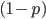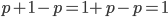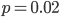I had a nice time at the Evolution meeting in Utah--this was my first Evolution meeting. There are some presentations that I attended that have stuck in my mind and I thought I should mention them here.
I attended a phylogenetics workshop on the first day. Joe Felsenstine (U. of Washington) gave a talk that segued from a historical overview to some current problems in phylogenetics. He gives entertaining talks that sometimes border on the cynical but are humorous. I especially liked his funding sources in the acknowledgements that included the Felsenstine foundation who's slogan is "instead of painting the house." On the more serious side he brought up the issue of inference of horizontal gene flow versus linage sorting in prokaryotes and archaea. There are several instances of horizontal gene transfer where DNA sequence has moved from one species to another in bacteria, but how many of these are actually "incongruent" lineage sorting in bacteria with very large ancestral species population sizes? On the other hand, rates of recombination in bacterial genomes are actually quite low, so if selective sweeps are frequent in bacteria (a later talk by R. Lenski is very relevant to this), perhaps effective populations sizes are indeed small and these are true horizontal transfers? He also brought up the possibility of looking at QTLs/heritability across multiple species to have power to get at what is under selection in correlated traits.
Brant Faircloth (UCLA) talked about using ultraconserved elements (UCEs) to reconstruct various phylogenies including helping to resolve the placement of turtles among birds and reptiles (which turns out to be an unresolved problem). There is a temptation to sequence and compare whole genomes of a range of species, especially since sequencing has become so cheap, but in the end a lot of the data is thrown out because it is hard to align, etc. There are various ways to focus down on smaller parts of the genome for comparison such as genome-wide exon (exome) sequencing from mRNA (exons are typically more conserved across species), DNA enrichment by sequence capture (seqcap) of exome DNA with tethered oligonucleotide probes, and finding variants around restriction endonuclease sites across the genome with RadSeq and RadTags. Another approach is to focus on regions that are highly conserved across a wide range of species (UCEs), there is a website dedicated to using these (http://ultraconserved.org/); these UCEs seem to contain a lot of binding sites for transcription factors that are deeply shared across metazoans (Ryu et al. 2012).
Later in the same workshop, Stacey Smith (University of Nebraska-Lincoln) gave one of the clearest, well organized, and informative (to the novice to phylogenetic inference) talks I have seen. (Many presentations I have seen on this topic have been cryptic and hard to follow, which often reflects a lack of detailed understanding by the people presenting.) She has also made her slides available online (link: http://www.iochroma.info/links) and said that anyone can use her graphics in their own presentations if they want! She went over parsimony, maximum likelihood, and Bayesian inference for discrete and continuous traits, the inference of relative rates of change and ancestral states and ways to visualize and interpret the results. Again, she gave an excellent presentation!
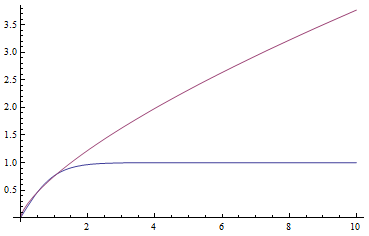
In a special address, Richard Lenski (Michigan S.U.) talked about some new results from his long term (25 year) artificial evolution experiment in E. coli. The experiment is now up to 50,000 generations and is still going. He has kept samples of the bacteria over the generations and can compare them to each other. One overall result is that fitness has been increasing over time from new mutations. Early in the experiment he thought the curve of fitness increase was hyperbolic, which asymptotically approaches a limit, but with more generations he showed that the change in fitness fits a power law curve significantly better, which does not have a limit. The implication is that fitness will continue increasing forever and will never reach a peak.
The image below compares an example hyperbloic curve, tanh(x), to a power law curve, (x/1.5)^0.7. The two curves may be similar early on, but diverge by a greater amount as time becomes large.
He also talked about the implications of one of his replicates that evolved citric acid metabolism. They screened a huge number of cells and did not see this occur again independently. But in the line where it did occur, if they went back to the generations just before this appeared, it did evolve again repeatedly (if I understood correctly what he was saying). There was also a great deal of evolutionary fine-tuning of the novel citric acid metabolism after it appeared. This demonstrated the steps of potentiation (setting the stage for a particular adaptation to be able to occur), actualization (the final mutant step that results in the new function), and refinement (additional changes to improve the system). They are working on nailing down the precise mutational steps that have happened in this lineage and a gene duplication (in citrate transport) is involved. He also discussed several lines of reasoning that this population of E. coli can be considered to have evolved into a new bacterial species--one of the defining features of E. coli is that it does not use citric acid as a carbon source, and intermediates have reduced fitness.
In other talks, Mingzi Xu talked about honest signals of fitness in male dragon flies. The dragon flies she works on use mie scattering of light (which also makes clouds white) from fat deposits on their wings to give them white bands that females are attracted to. The males don't seem to be able to cheat and produce a large white band if they are smaller and have less resources because the fat residue uses a lot of energy to create. She is going on to estimate heritability of the trait among offspring, etc.
Carl Bergstrom talked about "Timing of antimicrobial use influences the evolution of antimicrobial resistance during disease epidemics." Missing antibiotic doses extends the time it takes to get rid of infections--perhaps in a very predictable way--and missing doses early in a program is far worse that missing them later in a program in terms of the possibility of antibiotic resistance arising. I think this is because there are many more microbe cells present early in the program that could mutate to resistant varieties.
William Soto talked about "Adaptive Radiation of Vibrio fischeri During the Free-living Phase and Subsequent Consequences for Squid Host Colonization." Vibrio genus bacteria in Hawai'i are something I have become more interested in lately so I attended this to talk to get some more background information. Bioluminescent Vibrio fischeri are both free living in seawater and symbiotic with nocturnal bobtail squid; however, there may be different morphologies that are differentially adaptive in colonizing versus free living stages.
Benjamin Parker talked about immune response in aphids. They can generate winged and unwinged aphids that are genetically identical but develop differently and test how well they fight off infections. There is a cost to producing wings and the winged aphids also do not stop infections as well as the unwinged aphids; the immune response genes are not expressed as highly, etc. There are some parallels with costs of immunity in bumble bees.
Tyler Hether showed that the effects of mutations depend on the ways that genes interact (epistasis). The pattern depends on the type of regulation, positive or negative. This distorts the state space that can be traveled by a sequence via mutations so that change in some directions is faster than others as a function of the type of interaction among genes--the gene interaction network has an effect on the direction of evolvability. In general networks constrain adaptation; the space to transverse by mutations to get between states was larger with epistasis than the null model of no interaction between genes. This possibly relates to issues of phenotypic robustness despite mutational change in the underlying genes.
Benjamin Liebeskind gave a great presentation titled "Sodium Channels and the Origin(s) of Animal Behavior." This is a very difficult question to approach: what are the origins of animal behavior. Animals use sodium channels (similar to calcium channels), which also exist in protists, to create charge potentials and propagate signals along neurons. By looking at the gene sequences among species he found that these sodium channels predate animals who inherited them from common ancestors with modern protists. The channels started off as an "EEEE" holoenzyme, which evolved to a heterogeneous "DEEA" then a "DEKA" sodium channel holoenzyme. Interestingly there has been convergent evolution in cnidarians and bilaterians in sodium channel evolution and possibly origins of complex behavior?
Then I gave a presentation on engineering underdominance to transform wild populations (link to PDF of the slides). It was much more applied than the other talks but I still got some nice feedback from people that saw my presentation.
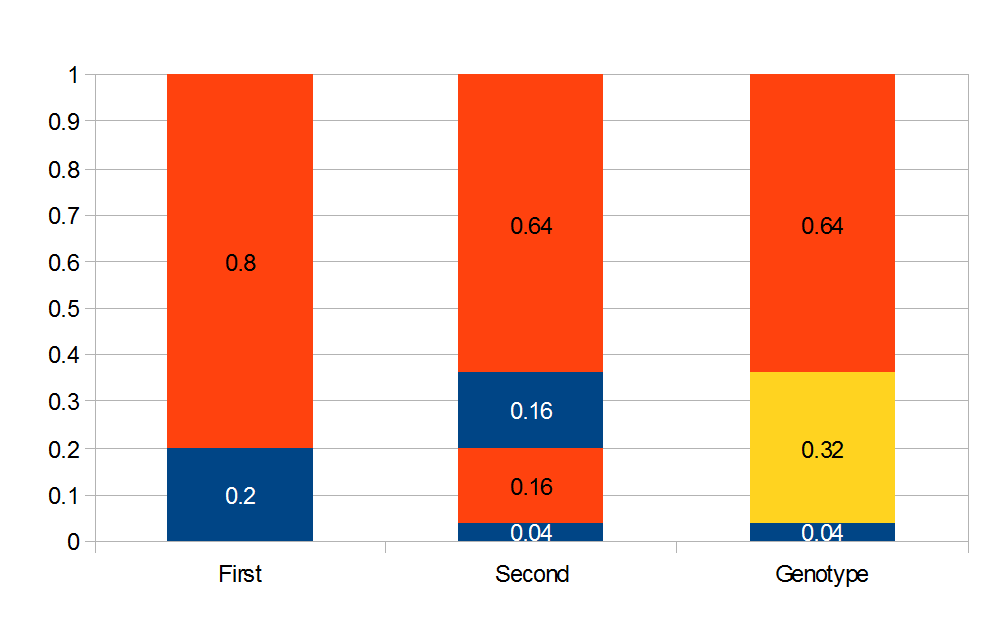
M. Slatkin (UCB) talked about inferring the number of genes underlying a complex trait (like stature that is influenced by many genes and the environment) from a very subtle signal in the covariance of the trait among parents and offspring. It requires huge sample sizes to work, on the order of thousands; however, these kinds of sample sizes exist for many traits. For example, each year I have my genetics class report height for themselves and their parents, if they can, to illustrate quantitative genetics (regression/heritability); this is a sample of about 200 each year so by the end of this fall I will have a total of about 600 parent offspring trios for a single trait. Perhaps the sample will be large enough in the coming years to use his approach with the students data to illustrate estimating the number of genes affecting the trait to the class?
Rebecca Chong (CSU) talked about rates of evolution in rearranged mitochondrial genomes. If I understood correctly, there is an acceleration of substitutions in genomes that have been rearranged, but this can not be explained by changes in mutation rate due to their position (single stranded DNA is more susceptible to mutation and the process of replication of the mitochonrial genome makes some areas single stranded longer than others) nor can it be explained by simple relaxation of selection (based on dN/dS ratios). So the question is, what is driving the changes in these genomes?
There was also a presentation followed by a question and answer session by program officers from NSF to explain more about applying for funding from NSF and some issues with the new application procedure. I appreciated them doing this and I learned some things, but honestly I did not get a lot out of it because I already read all the instructions, and follow them, for the application. Long story short--and they did not say this--we need to do a better job of petitioning congress (mailed letters, not emails, are the best way to do this) to provide funding to NSF. (I also received some comments back on my last application, but I will write about these in a later post.)
One talk that I missed that I really wanted to see was "The convivial origins of life on the Earth: A cooperative network of RNA replicators" by Niles Lehman (PSU). I have had a side interest in RNA evolution for a long time, but I couldn't be in two places at once... There were also a couple presentations about evolving robots that might have been fun to see, but the scheduling was bad for me.
Finally, there was a talk by Joan Strassmann (WU) on the discovery of bacterial farming in social amoebas. I liked the talk, but toward the end of the meeting things were starting to blur together. In a similar vein, I saw a presentation about strategies to minimize infections (undershooting versus overshooting a minimal infection threshold) during flu outbreaks--there is an interesting social (public versus private interest) conflict dynamic involved--but I can't remember now who gave the talk, sorry.
There were also poster sessions and one that jumped out at me was a poster by David Gokhman (HUJ) "Reconstructing the DNA Methylation Map of Extinct Human Species." Simplistically put, DNA methylation can "turn" genes "on" or "off." These are interesting because this process can explain a lot of things in genetics including trans-generational environmental effects on gene expression. There are ancient genomes that are being sequenced and Gokhman et al. used a mutation bias between methylated and unmethylated C's in the DNA sequence. (Methylated C's are deanimated to T's, unmethylated C's are deanimated to U's and lost from the sequence.) The Denisovan genome (lived until 30,000 years ago in Siberia and likely S. to S.E. Asia) was studied. Ancient methylated DNA sequences are, according to this mutation bias, expected to have higher C-to-T ratios and this can be compared to known methylation patterns in modern humans--the two are correlated. However they found 41 genes (e.g., EBP, HOXD9, UPF3B, NBEA, MAB21L1, miR-291-2, etc.) that are inferred to be differently methylated between the Denisovan and modern humans--these are genes affecting things like limb development and psychiatric disorders when they are disrupted.
There were also some displays related to teaching resources...(listed briefly here):
- HHMI BioInteractive stickleback evolution and gene regulation video (link). As well as some other videos.
- Junco http://juncoproject.org/videos/ an introduction to evolutionary studies in the junco. Videos are available online along with teaching resources.
- Quaardvark: https://animaldiversity.ummz.umich.edu/quaardvark/ to query the animal diversity database, can be used as a teaching tool.
There were no presentations Monday afternoon, so I went on an outing to the top of a nearby mountain (11,000 ft elevation) and took this picture of myself at arms length with my phone's camera (yes, that is snow in the background, in June). In the valley in the distance are the Sandy and West Jordan suburbs of Salt Lake City.


![Rendered by QuickLaTeX.com \chemfig{H-O-[:+75.5]H}](http://hawaiireedlab.com/wpress/wp-content/ql-cache/quicklatex.com-b91add6a2ca4b974da0008ad4f351e84_l3.png)
![Rendered by QuickLaTeX.com \chemfig{H^+-O^{-}-[:+75.5]H^+}](http://hawaiireedlab.com/wpress/wp-content/ql-cache/quicklatex.com-c99874556af3e4417f54e9029f254f93_l3.png)
![Rendered by QuickLaTeX.com \chemfig{H^+-O^{-}-[:+75.5]H^+-[::+0,,,,dash pattern=on 2pt off 2pt]O^{-}(-[:+104.5]H^+)-H^+}](http://hawaiireedlab.com/wpress/wp-content/ql-cache/quicklatex.com-0d6474b73c6dfb50cdcfeb360a129a9a_l3.png)
![Rendered by QuickLaTeX.com \begin{verbatim} \chemname{\chemfig{O=O}}{Oxygen} \chemsign{+} 2 \chemname{\chemfig{H-H}}{Hydrogen} \chemrel{->} 2 \chemname{\chemfig{H^+-[:-37.75]O^{-}-[:+37.75]H^+}}{Water} \end{verbatim}](http://hawaiireedlab.com/wpress/wp-content/ql-cache/quicklatex.com-814d1d7ef06286f1a1ab2eb8ab76810e_l3.png)
![Rendered by QuickLaTeX.com \chemname{\chemfig{O=O}}{Oxygen} \chemsign{+} 2 \chemname{\chemfig{H-H}}{Hydrogen} \chemrel{->} 2 \chemname{\chemfig{H^+-[:-37.75]O^{-}-[:+37.75]H^+}}{Water}](http://hawaiireedlab.com/wpress/wp-content/ql-cache/quicklatex.com-1a31e6d1d91c99772de53a85b7b294fd_l3.png)
![Rendered by QuickLaTeX.com \chemfig{C(-[:0]H)(-[:90]H)(-[:180]H)(-[:270]H)}](http://hawaiireedlab.com/wpress/wp-content/ql-cache/quicklatex.com-8f0d98d25779add44e95b35e16b58562_l3.png)


![Rendered by QuickLaTeX.com \chemfig{C(-[:90]H)(<:[:-9.75]H)(<[:-29.25]H)(-[:199.5]H)}](http://hawaiireedlab.com/wpress/wp-content/ql-cache/quicklatex.com-c6573ba7b47be31302f1428d735cc8b7_l3.png)
![Rendered by QuickLaTeX.com \setcrambond{2pt}{}{} \chemname{\chemfig{HO-[2,0.5,2]?<[7,0.7](-[2,0.5]OH)-[,,,, line width=4pt](-[6,0.5]OH)>[1,0.7](-[6,0.5]OH)-[3,0.7]O-[4]?(-[2,0.3]-[3,0.5]OH)}}{$\alpha$-D-Glucopyranose}](http://hawaiireedlab.com/wpress/wp-content/ql-cache/quicklatex.com-e060a85b20d841d498b22efb1a74105e_l3.png)
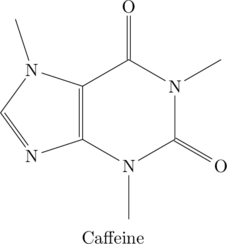
![Rendered by QuickLaTeX.com \begin{verbatim} \chemname{\chemfig{*6(C-N(-C(<:[:-9.75]H)(<[:-29.25]H)(-[:199.5]H))-C(=O)-N (-C(<:[:+129.75]H)(<[:100]H)(-[:-40.5]H))-C(=O)-C(*5(-N(-C(<:[:+180]H) (<[:+170]H)(-[:-307.5]H))-C(-H)=N-C=C)))}}{Caffeine} \end{verbatim}](http://hawaiireedlab.com/wpress/wp-content/ql-cache/quicklatex.com-245af7b42f9a5539f4226e37d9edc917_l3.png)
![Rendered by QuickLaTeX.com \chemname{\chemfig{*6(C-N(-C(<:[:-9.75]H)(<[:-29.25]H)(-[:199.5]H))-C(=O)-N(-C(<:[:+129.75]H)(<[:100]H)(-[:-40.5]H))-C(=O)-C(*5(-N(-C(<:[:+180]H)(<[:+170]H)(-[:-307.5]H))-C(-H)=N-C=C)))}}{Caffeine}](http://hawaiireedlab.com/wpress/wp-content/ql-cache/quicklatex.com-11bfed4cfad666d88537d3490df7fb87_l3.png)